Key points
• Complete reliance on cephalometric analysis for treatment may lead to suboptimal aesthetic results.
• Beautiful faces of different ethnicities have quite different shapes, but individuals of all ethnicities recognize them as beautiful.
• Faces that conform to the neoclassical canons are moderately attractive, but most attractive faces do not conform to these rules.
• In female faces, femininity is considered attractive, whereas masculinity does not necessarily signal attractiveness in men.
• Surface anthropometric measurements do not always correlate with the shape of underlying bone.
• Although some individual and cross-cultural differences exist, people seem to use similar criteria in their judgments of facial beauty.
History of morphometrics
Attempts to quantify and define facial attractiveness were made as early as 4000 years ago by ancient Egyptians and were further developed in ancient Greek society by applying the Golden Ratio to the study of ideal facial form. In the fifteenth century, these ideas were further developed to formulate the neoclassical canons of facial form by Albrecht Durer, Leonardo Da Vinci, and others. Today these ideas are still supported by many. Moreover, a Marquardt’s Phi Mask—a mesh based on the Golden Ratio—was developed to define facial beauty. However, its usefulness is controversial because the validity of the measurements to define facial beauty is still being debated.
Measurements
Modern morphometric analysis
Modern facial morphometric analytical techniques fall into two categories:
- 1.
Traditional morphometric analysis, based on lengths, widths, angles, ratios, and areas
- 2.
Geometric morphometric analysis, based on shape, using Cartesian landmark coordinates that capture the morphology of the face
Traditional morphometric analysis
Traditional morphometric analysis is based on the analyses of lengths, widths, angles, ratios, and areas. Until recently, all anthropometric analyses in surgery were based on these principles. Recording these measurements is time-consuming and is generally undertaken manually, using various instruments, including tapes, , scales, calipers, and Hertel exophthalmometers. The measurements require great precision and a degree of expertise to record and are open to both intra- and interobserver errors. Manual acquisition of anthropometric data is time-consuming and has limited the collection of large amounts of normative data. Moreover, most of the data relate to measurements of size, which tend to be highly correlated, and as a result, there are few independent variables. Furthermore, these data lack information on shape, which is a key property of interest.
Nevertheless traditional morphometric techniques form the basis of our understanding of the proportions of the human face, and thanks to the pioneering work of Leslie Farkas and others, large amounts of normative data are available. Traditional morphometric analysis is useful in plastic surgery and has revolutionized orthognathic surgery and orthodontics.
Many morphometric techniques are applicable to cosmetic surgery, but three deserve special consideration neoclassical canons, golden ratio and cephalometric analysis.
Neoclassical canons
Horizontal thirds
The face can be divided into thirds: (1) from the hairline to the midbrow, (2) from the midbrow to the nasal floor, and (3) from the nasal floor to the soft tissue menton. ,
Although the horizontal thirds were intended to apply across ethnicities, the proportions tend to be different across races: the middle part is shorter in white individuals and in black men ; and the upper third tends to be longer in black females, in contrast to the shorter upper third compared with the middle and lower thirds in Chinese females. Moreover, the proportions change with aging. Additionally, the lower thirds have more impact on the assessment due to incisor exposure and interlabial gap. This lower part can also be divided into thirds, with the upper one third from the subnasale to the stomion and the lower two thirds from the stomion to the menton, with a 30:70 ratio.
Vertical fifths
The face divides vertically into equal fifths (i.e., the width of one eye represents one fifth). The two most lateral fifths are measured from the lateral helix of each ear to the exocanthus of each eye. The middle fifth is measured between the medial canthi of both eyes (endocanthion to endocanthion). This distance is equal to the width of the nose. The width of the mouth represents 1.5 times the width of the nose. Similar to the case of the horizontal thirds, variations are seen. For example, with aging, the interocular distance and the nose width differ.
The neoclassical canons have been applied not only in art but also clinically. The use of these measurements is an easy, noninvasive attempt to define beauty; however, it lacks uniformity because it is not applicable to all ages, genders, and ethnicities. Additionally, the measurements need to be undertaken in a standardized, manual way and are highly prone to human errors. ,
Moreover, although faces that conform to these rules are considered beautiful, this method of measurement does not apply to all beautiful faces.
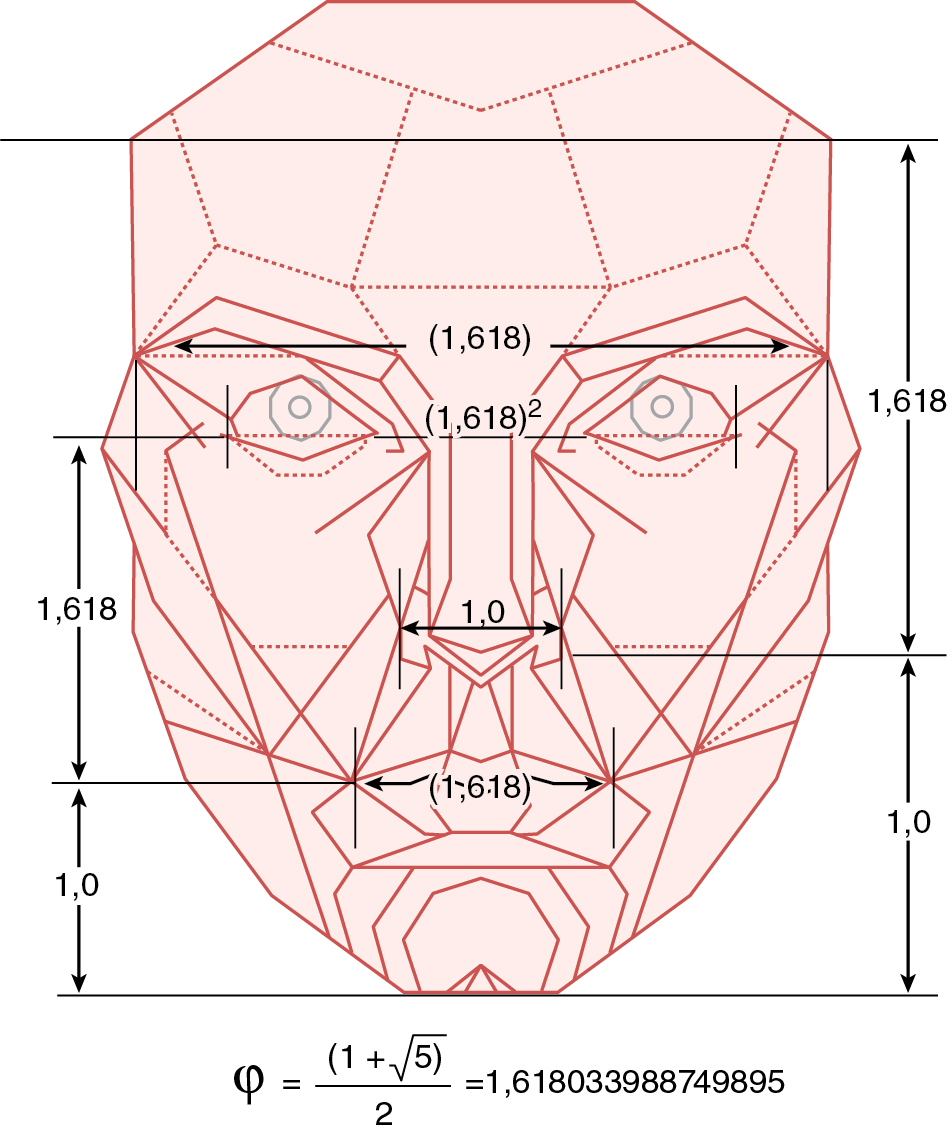
Golden ratio and marquardt’s mask
The concept of the Golden Facial Mask was proposed by Dr. Marquardt to define the perfect face with the use of a Phi mask—a mesh based on the Golden Ratio (1:1.618). Although artists have used the Golden Ratio successfully in the creation of their art, results of the use of this mask to define facial beauty in the clinic are controversial. The usefulness of the mask has been demonstrated in the assessment of the pre- and postoperative results of facial aesthetic surgery. However, on real faces, measurements using the mask are not always consistent when the values for different ages, ethnicities, and gender are not taken into account. Therefore gender-specific and race-specific masks are proposed on Marquardt’s website. However, the usefulness and application of the mask remains uncertain because, for example, faces that are considered beautiful (e.g., those of celebrities and fashion models) did not fit Marquardt’s Mask ( Fig. 3.1 ).
Cephalometric analysis
Cephalometric analysis can be used to analyze the facial skeleton, generally in a two-dimensional (2D) fashion and based on specialized lateral and anteroposterior (AP) skull radiographs (cephalograms). The technique was originally introduced by Broadbent, and since that time, many more complex analytical techniques have been introduced. Cephalometric analysis has many applications, including the following , :
- 1.
Diagnosis (e.g., assessment of the origin of a malocclusion—dental or skeletal)
- 2.
Description of patterns of facial symmetry and form—dolichofacial (vertical) and brachyfacial (horizontal), as well as the mesofacial (ideal) form
- 3.
Orthodontic and orthognathic treatment planning
- 4.
Monitoring of changes due to growth or treatment
- 5.
Prediction of orthodontic and orthognathic treatment outcomes
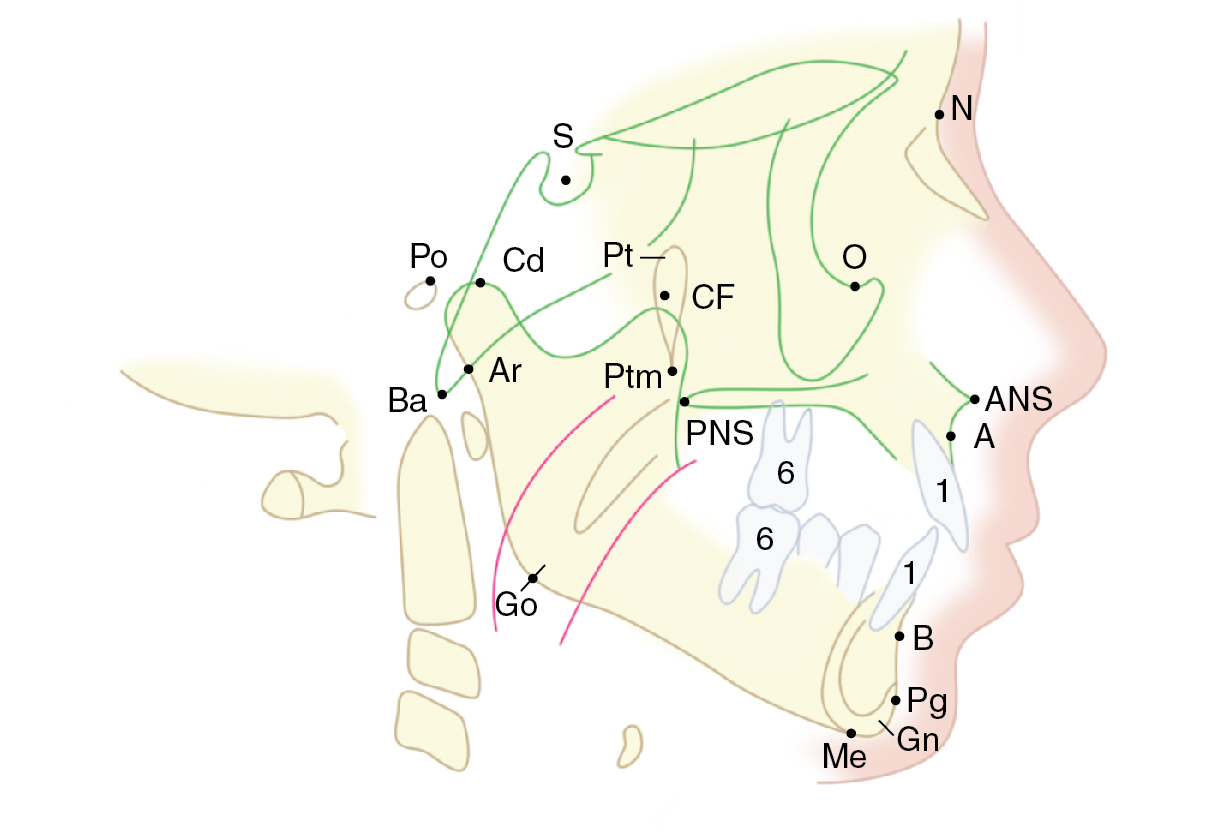
Anatomic landmarks.
The lateral cephalogram forms the basis of most types of cephalometric analysis. It gives key information about bony and soft tissue forms and how the two are related, as well as providing key information about vertical facial height and the AP relationship of the maxilla and the mandible. An analysis of the occlusion can be related to skeletal pattern. Generally the skull base (sella–nasion [S-N]) is used as a reference plane for analysis.
A lateral tracing includes the soft tissue outline, bony profile, outline of the mandible, posterior and anterior cranial base, odontoid process of the axis, anterior lip of the foramen magnum, clivus, planum orbitale, sella turcica, pterygomaxillary fissure, nasal floor, palatal roof, and body of the hyoid bone. The first permanent molars and the most central incisors are commonly included. Similarly landmarks are used for frontal tracings.
These cephalometric landmarks are used to construct planes. Sella–nasion defines the anterior skull base, which is used as a reference plane, with the nasion as a reference point. The Frankfurt horizontal plane (orbitale–tragion) is placed exactly horizontally to define the neutral head position. Other important planes include the mandibular and palatal planes. The angles at which planes intersect provide further information about facial form.
Lines and angles to evaluate soft tissue.
Several lines and angles can be created on the basis of anatomic landmarks to evaluate the facial soft tissue. These include the convexity of the face, formed by the soft tissue glabella, subnasale, and soft tissue pogonion; chin position, using the meridian line, formed by a line perpendicular to the Frankfurt horizontal plane passing through the nasion soft tissue; and the ideal position of the lower lip. , Moreover, the facial profile has been described according to the Steiner aesthetic plane and the Riedel plane. A Powell analysis, which is made on the basis of the nasofrontal angle, nasofacial angle, nasomental angle, and mentocervical angle, can provide insight into an ideal facial profile. All these measurements describe the ideal profile based on average values. Although they are useful analytical tools, the values provided by them should not be regarded as treatment goals in aesthetic surgery, where averageness is not necessarily the desired outcome.
Occlusion, dentition, and skeletal relationship.
An understanding of occlusion not only is essential for orthodontic and orthognathic treatments but also plays and important role in aesthetic surgery. The relationship of the anterior teeth to the lips and surrounding soft tissues has a significant effect on lower facial form.
The anterior–posterior (A-P) relationship of the incisors is affected by skeletal pattern and incisor inclination. The skeletal pattern (class I: normal; class II: mandible retruded relative to maxilla; and class III: mandible protruded in relation to the maxilla) is measured by using the skull base plane S-N to the A (SNA) and B (SNB) points on the anterior maxilla and mandible. Abnormal skeletal patterns can exist due to over- or underdevelopment of the maxilla and/or the mandible. The angles SNA and SNB indicate in which jaw the abnormality lies. The angle ANB (A point, nasion, B point) defines the skeletal pattern ( Figs. 3.2 to 3.4 ).
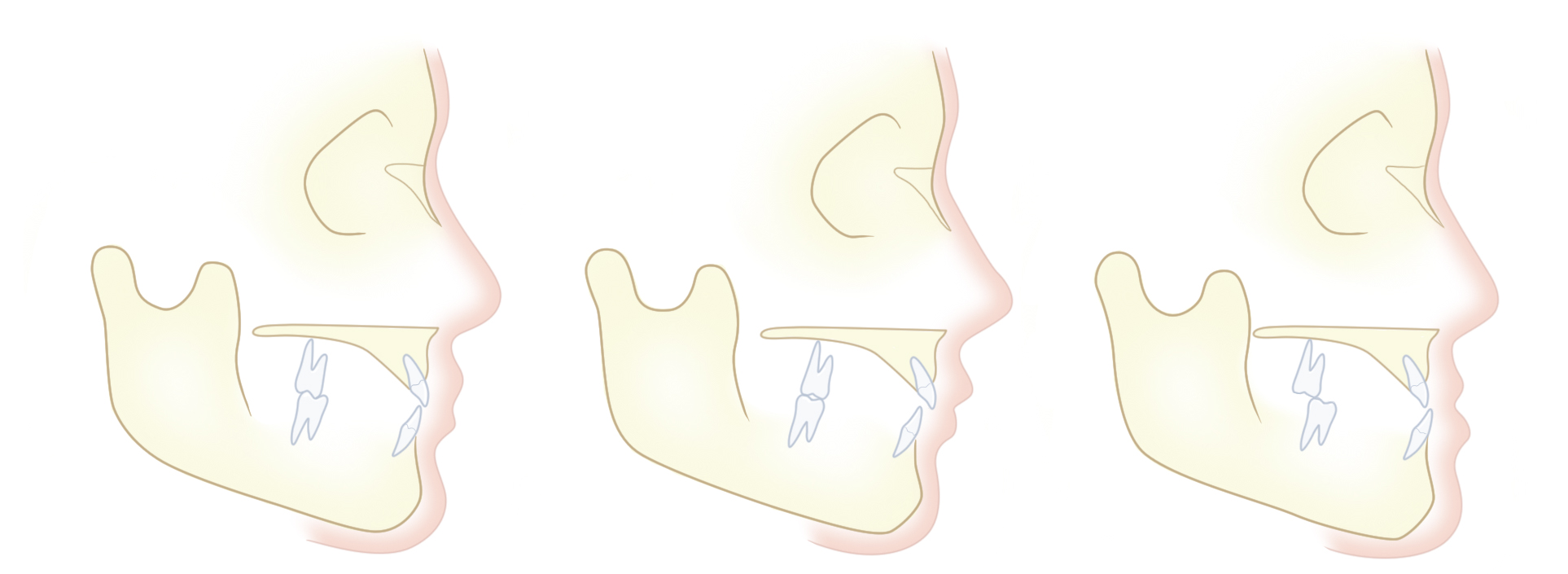
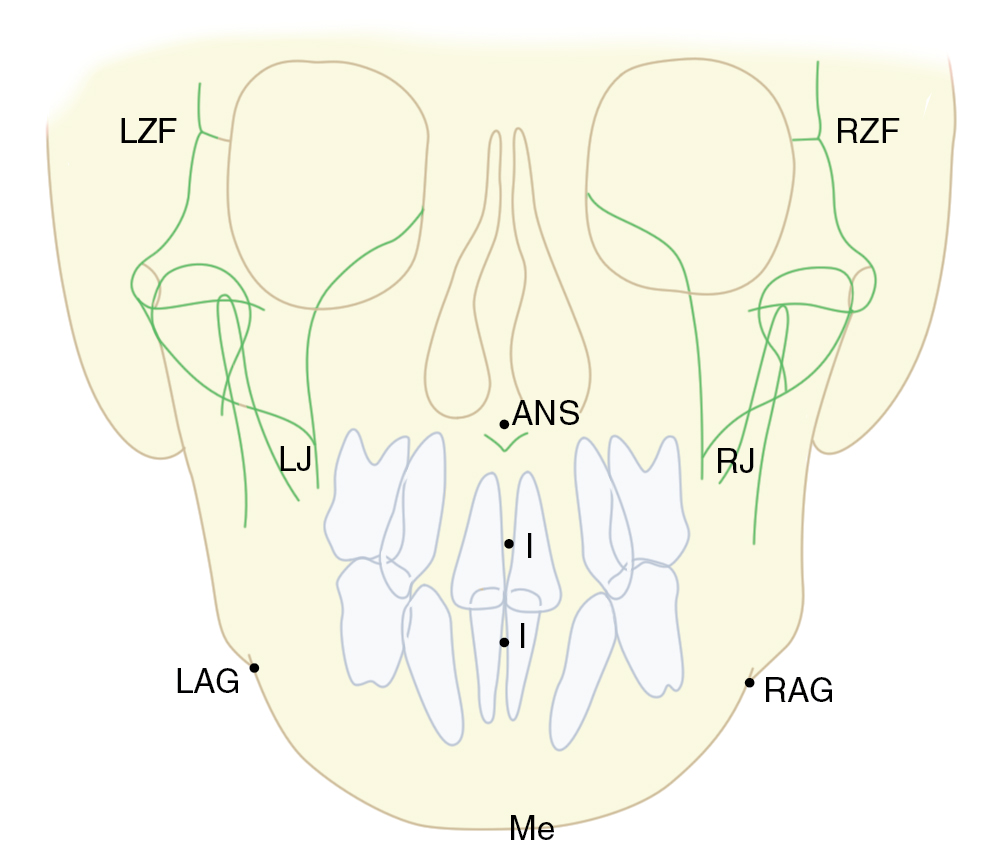
The A-P relationship of the incisors is similarly classified in classes I–III, and in addition, the incisor inclination is measured relative to the maxillary and mandibular planes.
An understanding of these relationships is key to treatment planning and will indicate whether treatment can be undertaken by orthodontics alone or by surgical treatment, such as orthognathic surgery or masking procedures (e.g., implants).
The vertical proportions of the face can also be determined by performing cephalometric analysis, which can indicate where in the face vertical excesses and deficiencies exist. This is often overlooked. Understanding vertical discrepancies in the face is a key factor in planning bone surgery and will affect the outcome and stability of surgery.
Computerized cephalometric diagnosis and treatment planning.
Currently, tracing can be done digitally using a dedicated interface, but the method (2D manual tracing) remains the same. Although cephalometric analysis has been proven to be successful and useful, it may be misleading. There exist numerous disadvantages. First, the value of the analysis depends on the accuracy of the landmark identification. Second, in the case of accurate landmarking, the right number of landmarks are essential because the fewer the markers used in the tracing, the greater is the risk of misdiagnosis. In addition, complete reliance on the cephalometric analysis for treatment planning can lead to aesthetic problems , , because occlusion and facial beauty are interdependent. , Last, an optimal cephalometric result might not translate directly to an optimal soft tissue result.
Geometric morphometrics and statistical shape analysis
Geometric morphometric analysis studies shape by using Cartesian landmark coordinates, rather than linear, angular, or volumetric variables, to capture the morphology of the face. The techniques have had a major impact in anthropology but are relatively new to facial analysis.
Facial three-dimensional (3D) data may be acquired by using computed tomography (CT), magnetic resonance imaging (MRI), stereophotogrammetry, laser scanning, and handheld structured light scanners.
Statistical shape analysis (SSA) is the field that involves methods for analyzing the shapes of objects by means of statistical methods. In this field, shape is defined as the geometric information that remains when translation, rotation, and scale effects are removed. SSA has been used successfully to solve a wide range of practical problems and applied in many disciplines, such as computer vision, machine learning, and medical imaging.
The process of building a SSA model consists of collecting a training set of objects whose shapes need to be examined; aligning the objects to a common template by removing translation, rotation, and scale (alignment); bringing every object into dense correspondence (registration); and, finally, analyzing the statistics of the distribution of the new registered shapes. The aforementioned process is the same for cases of both 2D and 3D shapes. In this chapter, we focus on the case of SSA for 3D human faces.
Blanz and Vetter pioneered the use of SSA for 3D human face shapes with the 3D Morphable Model (3DMM). In their seminal work, they built a 3DMM by applying principal component analysis (PCA) in a set of 200 registered subjects of a similar ethnicity and age. 3DMMs are powerful statistical models because they are generative models (i.e., they can generate new instances of face shapes that are not in the initial data set).
Since its first appearance, various 3DMMs have been proposed. The Basel Face Model used a data set of 100 males and 100 females. These models do not contain enough subjects to fully describe a population. This issue is partially amended by the Liverpool-York Head Model of 1200 distinct identities, which is a craniofacial model. The problem was finally addressed by the Large-Scale 3D Morphable Models (LSFMs).
Large-scale facial models
LSFM is a 3DMM automatically constructed from nearly 10,000 faces, the largest 3DMM model ever constructed. This model is trained on rich demographic information, with a significant variety of ages, genders (48% male, 52% female), and ethnicities (82% white, 9% Asian, 5% mixed heritage, 3% black, and 1% other), allowing for the construction of models specific for age, gender, or ethnicity.
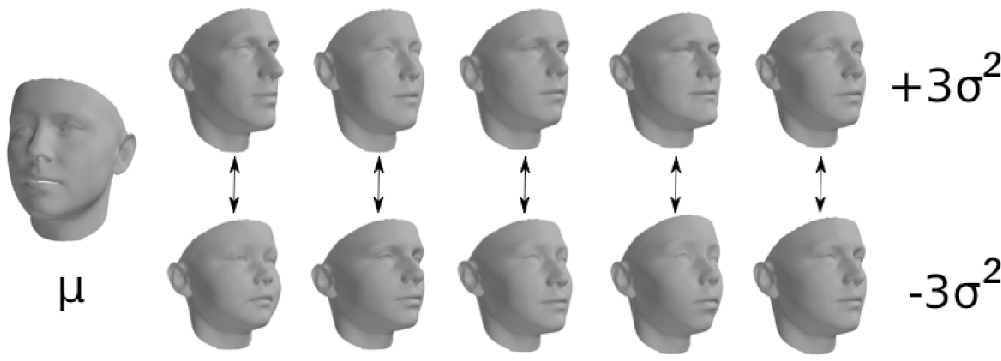
As LSFM is extremely diverse with regard to age, gender, and ethnicity, a bespoke 3DMM for each group can be formulated. Fig. 3.5 shows the mean face of the global model and some bespoke models for various groups, with the first five modes of variation. Fig. 3.6 illustrates clearly the differences in facial shape with increasing age. Figs. 3.7 and 3.8 demonstrate that different mean and modes can be seen in gender- and ethnicity-specific models. Fig. 3.9 shows the ethnic differences on a texture model, including the five components. Using T-distributed Stochastic Neighbor Embedding (t-SNE), a visualization of the face shapes in two dimensions can be made. In the left subfigure of Fig. 3.10 , a clear trend of increasing age can be noted. The right subfigure shows that the three ethnic variations create three distinct clusters.


Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree