EVALUATING THE DAMAGE, PROTECTION
AND REPAIR OF HAIR
Authors
Ray Rigoletto Sr. Manager, Global R&D Applications Care Specialties: Hair Care; Home Care
Ashland, Inc.
Tim Gillece
Ashland, Inc.
1005 US Hwy No. 202/206 Bridgewater, NJ 08807
ABSTRACT
Human hair is continually exposed to various damaging factors that result in a negative impact on its cosmetic properties. Common sources of hair damage include daily use of shampoo detergents and normal grooming processes. In addition, there are more severe sources of damage. These consist of weathering from the UV-Visible components of sunlight, the action of chemically active hair products (such as oxidative hair dyes, hair relaxers, permanent waves), and the use of thermal styling appliances to create extreme hairstyles.
In order to understand the mechanism of the damaging process, as well as the actions of treatment compositions that protect or repair damaged hair, appropriate test methods need to be employed. These methods allow the study of hair from the macroscopic level (where whole hair attributes are assessed) to the determination of changes at the morphological and molecular levels. This chapter describes frequently used test methods for evaluating fiber damage and demonstrating the efficacy of protective or repair treatment systems.
11.4.2 The nature of hair damage
3. Color wash-fastness techniques
4. Mechanical and thermal-mechanical damage
11.4.4 Instrumentation and experimental methods for studying
damage and protection of hair
1. Differential Scanning Calorimetry
2. Surface Tension, Wetting, and Contact Angle Analysis
5. Time of Flight-Secondary Ion Mass Spectrometry (ToF-SIMS)
6. X-ray Photoelectron Spectroscopy (XPS)
7. Inverse Gas Chromatography (IGC)
3. Scanning Electron Microscopy (SEM)
4. Atomic Force Microscopy (AFM)
7. Dynamic Mechanical Analysis
f. Infrared Thermography (IRT)
a. Color wash-fastness of oxidative hair color from
shampoo stripping
2. Image analysis of digital photographs
b. Color Protection from UV-Induced Fading
e. Strategies for permanently repairing hair
a. Panel testing: shine; color; combing; feel
b. Fiber fragmentation techniques
“I am under a lot of stress” is a frequently heard complaint. Despite the advanced technology that tries to make our life easier, such as microwave ovens, dishwashers, voice-controlled devices, and the like, we still suffer from too much to do and trying to accomplish it all under a limited time frame. But, semantically speaking, are we actually under stress? Rather, it can be argued that we are being strained. Strain is an outside influence such as an ominous deadline that must be met and stress is our reaction to the applied strain. Some people are frazzled by life’s complexities, whereas others can inherently adapt to more strain. Consequently, one’s tolerance for internally felt stress is unique to factors such as the current psychological, biochemical, and social states of the individual. We can all relate to this on a human level; but in order to fully relate to the impact of stressors on hair it is imperative to gain an understanding of the physical relationship between stress and strain.
The relationship between stress and strain depends on whether force or distance is used to probe a material. If strain, or deformation of a material, is the mode of action, then stress in the system is the reactionary response. If stress, or force per unit area, is the mode of action, then the degree of strain is the measurable response. A simple model can demonstrate this easily. Take a rubber band and stretch it. The distance, or strain, applied to stretch the rubber changes the way the atoms in the solid are assembled. In reaction, the new physical configuration of the rubber band affects the resistance (i.e., stress response) to the applied deformation. Ultimately, at a critical strain, small irreversible fissures in the rubber begin to form, and applying further strain to the band induces stresses that ultimately cause a catastrophic break in the rubber.
During the course of explaining some of the test methods to determine the mechanical properties of hair, there will be stress-controlling devices that monitor changes in physical dimensions, and strain-controlling devices that measure the stress response of the deformed fiber; however, stress and strain do not have to be mechanical in nature. It is conceivable to expand the definition to include factors such as chemical, thermal, and environmental insult. In analogy, there are different limits to individuals tolerating a polluted city, or to resisting the sweltering heat, and ultraviolet radiation of the summer sun.
The subject of this chapter deals with human hair and the many factors that subject hair to stress. These include the various chemical and thermal treatments applied to hair in order to improve its cosmetic appearance, as well as environmental factors, especially UV radiation from the sun. The integrity and physicochemical state of the hair impacts the resilience of the fiber and its coinciding resistance to stress. Obviously, if the hair is compromised in some way, either chemically or structurally, it will not hold up to subsequent treatments.
An example of stress put upon hair by the strain of environmental conditions is the work done by Ratnapandian et al. where they studied the mechanical properties of hair after exposure to a controlled dose of solar radiation [1]. As reported by the authors (see Table I) the hair strength is compromised, as indicated by a positive percent loss in mechanical properties. The increase in the magnitudes of the turnover point (defined in Table I) and strain to break, as indicated by a negative percent loss values, actually represents hair weakening since they are due to the breakage of disulfide cross-links that consequently increase the mobility of the molecular chains. A full description of the mechanical properties of a hair fiber from the stress-strain curve and the molecular changes that occur at each stage can be found in Feughelman’s treatise on the subject [2].
Table I: Percent loss of mechanical properties of hair with simulated solar radiation (300 hours; 70% RH). Data from Ratnapandian et al. [1].
Mechanical property from stress-strain curve | % Loss |
Work to 20% extension | 46.51 |
Stress at 20% strain | 43.18 |
Initial modulus | 46.69 |
Post yield modulus | 60.63 |
Work to break | 23.14 |
Stress to break | 49.06 |
Turnover point* | – 36.54 |
Strain to break | – 43.14 |
* The intersection of the yield and post-yield part of the elongation curve; see Figure 42b.
In this experiment, the treatment of hair with a controlled time and intensity of solar radiation exposure is an example of straining the fiber, with weathering as the active agent. Also, the measuring device for evaluating the mechanical properties, which in this case is the tensile strength tester, is also a strain-controlling device since the rate of deformation imparted to the hair fiber is held constant.
In order to study the nature of hair damage from the multitude of strains and the consequent stressful factors that it is subjected to, as well as determining the efficacy of ingredients and ultimately products for protection and repair, appropriate test methods need to be employed. This is not a simple task. Hair has a very complex chemical makeup and morphology, and the imparted stresses and strains vary as a result of the type of cosmetic treatment being employed.
This chapter provides an explanation of the nature and utility of methods that are used in the assessment of hair damage, its protection, and repair. Methods are described in enough detail for the cosmetic chemist to utilize them appropriately and to make sound conclusions from the generated data. Sometimes an understanding of the damage mechanisms can be achieved with one method; however, it is prudent to use a combination of methodologies to build a case for proving product efficacy, especially with regard to claim substantiation. Throughout the course of explaining each method, an underlying theme is to keep in mind whether the stress-strain relationship is physical or chemical in nature. With regard to human hair, it will provide a reference for understanding the factors in the degradation of hair, its interaction and response to cosmetic ingredients, and the measurement of these effects with appropriate test methods.
11.4.2 THE NATURE OF HAIR DAMAGE
The major stresses that hair experiences are:
- 1. Shampoo fatigue—The distal ends of shoulder-length hair could be up to two years old and have gone through literally hundreds of shampoo cycles. Even if a mild shampoo had been used during the course of the lifetime of the hair, the surfactant slowly extracts the lipid of the hair as well as smaller-molecular-weight fractions of protein that are the result of other damaging treatments. This slow erosion of hair compromises its structural integrity over time.
- 2. Mechanical Damage—Combing or brushing of hair imparts shear stresses within the fiber. As a comb is pulled through a tress in the direction from root to tip, the bending of the hair fibers is also forced to propagate from root to tip. That is, it is a dynamic bend and not a static one. These shear stresses produce fine fractures within the interior of the cortex, which upon further combing, result in either a split end, or worse still, breakage. Compression, tensile, and torsional forces are also present from continual bending and add to the stresses at work during combing and resultant fracture. The situation of fracture becomes magnified when hair is in the wet state. Hair that is wet is more extendable due to changes in hydrogen bonding between adjoining structural protein elements of the hair. Mechanical stress, such as towel drying or combing out a snag in the wet state, will also cause breakage.
- 3. Weathering—Sunlight affects hair in several ways. Light of shorter wavelengths and higher energy, designated as UVB, degrades disulfide bonds as well as structural components of the hair such as the lipids of the CMC. Once these are degraded, important hair attributes are compromised, resulting in a decrease in cosmetic effects, including shine and elasticity. The natural pigments of the hair, eumelanin and pheomelanin, defend against this by absorbing UV light and protecting the chemical components of the hair. Hair that is light in color, such as natural blonde or bleached fibers, does not have this natural defense and is more prone to damage.
- 4. Chemical processing—The chemistry of bleaching, oxidative hair dyeing, permanent waving, and relaxing have been well described in the literature; a recommended reference is by Robbins in The Chemical and Physical Behavior of Human Hair [3]. All of these chemical treatments have multiple damaging effects on the structural components of hair. When chemical bonds are broken, functional groups change their character and influence the cosmetic behavior of hair. One example is the removal of the lipid layer from the surface of hair, which is essential for important hair attributes. Another is the formation of cysteic acid groups, which makes hair more hydrophilic, and decreases hair characteristics such as detangling and hair manageability. Many other examples can be cited based on the varied chemical components of the hair.
- 5. Thermal Styling—Styling appliances configure hair through both mechanical manipulation and heat. Examples of these include curling irons and flat irons. It will be shown in this chapter that the excessive heat induced by these appliances tends to denature structural proteins in the cortex and cuticle of the hair. Although this treatment initially imparts attractive cosmetic effects, with continued use the hair becomes less manageable and suffers from a decrease in its cosmetic appeal. The result is that the consumer has to use intensive conditioning treatments to conceal the damage.
- 6. Thermal/mechanical (wet to dry styling)—After adding a styling gel or cream to damp hair, it is usually styled with a round brush and blow dryer. The subsequent insult is not only from the heat of the blow dryer, but also from the brushing process. Combing and brushing are damaging to dry hair, but when hair is wet, it is in a weakened state and is more prone to breakage during combing. If the styling product goes through a tack phase, brushing becomes very difficult and results in a large extent of breakage.
Damage imparted to hair can range from the molecular level, to the subassemblies of the fiber. The deterioration alters the complex structure of proteins in the microfibrils of the cortex and extends to macroscopic structures, including the cuticle and cortical cells. There are test methods appropriate for studying hair damage at each level. The ultimate level is observing changes in damage impacting whole hair attributes, where many fibers interact as an assembly. Cosmetically acceptable attributes from fiber interaction include, for example, curl definition, body, and shine; whereas the damage state exhibits a host of negative attributes including frizziness, poor comb through, and dullness.
Unfortunately, the state of hair is a bleak one since it cannot renew itself. As the dead fiber suffers more and more stress, there is a vicious downward trend until the fiber fractures and breaks. Since hair grows from the scalp, the hair’s age increases along the fiber from root to tip so that the tips usually have the highest degree of damage. As hair is combed, the shear stresses imparted to the hair will be most destructive to the ends, with the result that the ends will fracture or produce split ends. Therefore, a fiber’s ability to respond to multiple stresses depends on its current level of damage. Another factor is the morphology of hair. Since hair is a biological outgrowth of the expression of a person’s genes, each individual then has a different hair type. In general, hair can be categorized by racial descent so that Asian hair is characterized by a larger diameter, and Caucasian hair is generally finer. Of course there is overlap of hair types between the races, but it can be concluded that morphological differences allow hair to be more or less hardy in its ability to handle the stress of damaging treatments. For example, during the use of a curling appliance, the thermostat has to be put on high to “curl-up” the larger diameter of Asian hair.
If hair was a living structure, then certain treatments may rejuvenate the broken structures so that hair can revert to its undamaged natural state, such as when it first emerges from the follicle. Unfortunately, this strategy cannot be employed and consumers resort to treatments that condition, protect, and what is more challenging, repair damaged hair so that they can continue with their usual styling behaviors. Some of these treatments are cosmetic and temporary in that the results from the treatment are usually washed away in a subsequent shampooing. Protective treatments help hair to take the insult of aggressive styling processes, such as hot flat ironing, so that damage is alleviated and the breakage of hair is postponed to a later date. But again, based on the dead nature of hair, its fate is sealed; ultimately there will come a day when the hair fiber will break.
Luckily, from a biological standpoint, there is hope. Each fiber is constantly renewing itself by generating new hair inside the follicle. Those follicles that are most active, those that are in the anagen phase, are producing keratin cells that mature in the follicular canal and then emerge from the scalp in its natural undamaged state, only to be cast into the world to suffer the stresses and strains of wear and tear.
The manner in which hair is artificially damaged, and with respect to what has been described above, imparting a controlled strain on hair, depends on the particular objective of the experiment. Once the goal of the experiment has been established, then the scientist designs the experiment to maintain control of important variables. For example, some variables are held constant and one or more variables are purposely manipulated with the primary intent of determining effects.
For each of the stresses that hair suffers from, a treatment can be designed to simulate the stress. These are usually performed on hair tresses of a particular configuration and hair type, such as fine or bleached fibers, for example. These treatments can be termed treatment regimen because the tress is purposely exposed to successive treatments that simulate what a consumer would do in real life. A simple example would be to wash and dry a hair tress with a shampoo to determine the damaging effects of the surfactant after multiple washes. Damage can be assessed periodically during the course of washing using, for example, a Scanning Electron Microscope to determine the state of the cuticle. Also, contact angle measurements with a tensiometer will indicate to what extent the protective lipid layer of the hair was extracted by the detergent of the shampoo. More complicated treatment regimens have been designed to study the effects of other strains on hair. Several examples from the literature will follow that have been utilized for assessing the effects of UV degradation by sunlight, thermal effects from appliances, color wash-fastness of permanently dyed hair from multiple washing cycles, and mechanical fatigue. These will serve as examples to demonstrate how to design a treatment regimen to study the effects of the key variables under study. These should not be considered as standard procedures, but as part of the experimental design to control and manipulate variables to determine effects.
Hot flat irons that are used to produce a straight style can reach temperatures of up to 450°F. The styling procedure consists of taking about an inch-wide section of hair and applying the hot iron close to the root section and moving the iron from root to tip without hesitating. This procedure is continued until all of the hair on the head is treated. The thermal insult to hair can be done on hair tresses in order to run controlled experiments. A treatment regimen can consist of first washing and then treating the hair with a pretreatment to study its effect on alleviating the damage incurred to the hair from the hot ironing process. After the hair is dry, the hot flat iron is heated to a specified temperature. Then, in a controlled fashion, the iron is applied to the root section of the hair and moved down to the tip in a specified length of time. This is repeated a number of times to achieve a total time of heat exposure. Intermittent shampooing and re-treating with the experimental composition can be done as well. Measurements are taken initially, during the course of the treatment regimen, and then at it end. Alleviating damage of the hair due to the experimental composition can be determined by comparing results versus an appropriate control. A treatment regiment is illustrated in Figure 1 that was utilized by Zhou et al. to study the thermal-protective effects of polymeric pretreatments and their alleviation of hair damage resulting from the hot ironing process. Methods utilized, which will be described in more detail in a subsequent section of this chapter, were Differential Scanning Calormetry (DSC), a specialized anti-breakage method, microscopic techniques, FTIR spectroscopic imaging, Dynamic Vapor Sorption (DVS), and thermal image analysis [4]. Results from this work indicated that several synthetically derived polymers were effective in thermal protection, especially those that were hydrophobically modified.

Figure 1: Treatment regimen used in the thermal insult of hair tress to study thermal damage and effects of protective pretreatments.
A similar treatment regimen was designed by McMullen and Jachowicz [5] in their efforts to study the effects on alleviating the damage to hair from curling irons. Again, the methodology consisted of exposing the hair to the heat from the curling irons for periods of time with intermittent shampooing and re-treating with the protective composition. However, in this case the mode of exposure of the curling iron was different than that of a flat iron in that the curling iron was clamped onto one section of the hair for a specific period of time. The window of exposure was then assessed to show the damaging effects of the heat as well as the alleviating effect of the pretreatment composition. This was accomplished by detecting a reduction in combing forces as tested through a mechanical combing device, and a reduction in the level of Tryptophan, an indicator of hair damage, by spectrofluorimetry.
There are many manually operated parts of the hot ironing process that are a source of variability in thermal treatment regimens. Maintaining a constant rate of descent of the hot iron from the root to the distal part of the tress is very difficult, especially if the polymer treatment on the hair creates a drag for the iron. The tension that the operator applies when pressing the plates of the iron against the bundle of fibers is a compound variable. As the operator uses more force to press the jaws of the iron against the fiber bundle, more force is applied to pull the iron down the tress to keep the rate of descent constant. This results in the fibers being stretched longitudinally. To control and monitor these variables, an automated apparatus was designed by Dussaud [6]. It consists of a tress mounted on the arm of a texture analyzer so that the rate of movement of the tress in relation to the hot flat iron is controlled. The two plates of the iron are brought into contact with the bundle of fibers and the tension is monitored by a force sensor. The stretching force is kept constant, as measured by the texture analyzer, by applying a certain contact force of the iron jaws against the hair. Hair temperature is monitored by the use of an infrared thermometer. Measurements by Dussaud after controlled thermal treatments with this automated apparatus included DSC, wet elasticity, and birefringence [6]. From this study, interesting conclusions on the permanent straightening of curly hair are described.
References in the literature indicate that solar exposure degrades various components of the hair. These changes affect lipid components [7] and proteins [8]. Other aspects of the photodegradation process include understanding the role of melanin [9] in photoprotection, as well as other variables including moisture [1] content, and the degree of damage through processes such as bleaching, perming, and dyeing with an oxidative hair color [10].
A key piece of equipment requisite to performing a UV exposure study is a solar simulator. One could subject hair tresses to natural sunlight; however, variations in cloud cover, sun angle due to the time of day, as well as change of season, puts many obstacles into performing a controlled study. The solar simulator allows the experimenter to control important variables such as light intensity, wavelength, temperature, and humidity. The simulator consists of a light source such as a Xenon lamp, a filter that will subject the hair to a particular part of the electromagnetic spectrum, and a chamber that can control temperature and preferably humidity as well. The filter will allow simulation of normal daylight, or in more refined studies allow just certain bands of UV light to impinge on the hair such as UVA, UVB, or a combination of both.
As with thermal degradation, photodegradation studies also follow a treatment schedule. The experimenter will shampoo and pretreat the hair with a protective composition and then expose the hair for a certain length of time while keeping necessary variables, such as temperature, humidity, wavelength, and radiation intensity, held constant. The treatment and exposure cycles are usually repeated to represent the most practical consumer use conditions. In this way Locke studied the effect of a substantive UV photofilter by treating tresses with a protective composition and then putting the tresses into a sample holder that had an exposure window. Tresses were treated and exposed for eight hours. This was repeated for a total of 32 hours of exposure. Exposure consisted of placing tresses in a weatherometer that had the irradiation adjusted to simulate the same intensity of sunlight found during the day in Florida in April. Measurements were taken in the exposed and unexposed regions of the tress to determine and compare the degree of photodegradation and resultant protection by the UV photofilter. Measurements in reduction in combing and tryptophan degradation were conducted [11].
There are many references to help the experimenter with designing a protocol for study. One is by Signori where the author reviews the current understanding of the effects of ultraviolet and visible radiation on hair structure and options for photoprotection. Among some of her advice, she mentions that correlating the length and intensity of the simulated light to real-world conditions is an important factor to consider [12]. Also, many questions can be answered by referring to one of the manufacturers of the solar simulator [13].
3. Color Wash-fastness Techniques
Peroxide containing oxidative hair color is designed to “lift” the natural color of the hair and at the same time react dye intermediates inside of the hair. The intentions of this process are primarily for covering gray and/or changing one’s natural color from brown, for example, to red. Although these products are termed permanent, a certain amount of fading takes place due to continuous cycles of washing and conditioning. Primarily, this is due to the surfactants used in these products that tend to slowly leach the water-soluble artificial pigment or dye out of the hair. This results in a change in both the intensity and hue of the hair, which is unacceptable for a consumer. Many products on the market consequently claim retention of the vibrancy of color with the use of protective ingredients.
To design a treatment regimen to test for color wash-fastness, hair tresses are typically first dyed and then cycled with a regimen of products. The regimen consists essentially of a shampoo, and may be followed by a conditioner and leave-in styling/conditioning products. Color measurements are then taken throughout the treatment cycle and measurements are compared to the initial state of the hair. Percent protection of the product in question is determined by comparing to appropriate controls. Such a treatment schedule was utilized to determine the color wash-fastness effect of a hydrophobically modified polymer in a treatment regimen of shampoo, conditioner, and leave-in treatment. In this case, bleached hair was dyed red, a color that is most prone to fading from shampooing, and cycled with a regimen of formulas both with and without the hydrophobic polymer. Results were substantiated with colorimetry measurements and image analysis. More sophisticated methods were used, such as water contact angle and FTIR spectroscopic imaging, to help propose a theoretical mechanism of action of the active ingredient [14].
4. Mechanical and Thermal/Mechanical Damage
Combing imparts mechanical strain to hair, i.e., hair gets stressed by the strain of combing. There are different components to this stress. Figure 2 illustrates a hair tress being pulled through a comb that is being held stationary under a stereomicroscope. The various strain components are labeled and consist of shear stresses in the internal parts of the hair through dynamic bending, i.e. bending that is propagated from root to tip, longitudinal tension though extension, abrasion, impact loading, compression/expansion through bending, and torsional strain. As Figure 2 illustrates, the combing process will include all of these strains. Specialized instruments have been designed and employed to isolate and test each component or combination of components of the multiple mechanical stresses that hair is subjected to during grooming to determine their effects on hair damage. The strength of hair, and in the case of cosmetic treatments, the alleviation of weakening of hair with its consequential breakage or reduction in cosmetic attributes, is quantified after a set regimen of specific strains. These strains can be designed to be in a longitudinal (tensile), radial (torsional), or tangential (bending) direction. Abrasion and impacting are other components that have been studied. One complicating factor is that other stresses, such as chemical, UV, and thermal exposure, tends to weaken the hair so that there is a greater propensity to break under mechanical strain. Many treatment schedules found in the literature, therefore, have as their regimen a combination of these stresses imparted to the hair. The application of these stresses as described in the literature will be described in the next section.

Figure 2: Mechanism of Hair Breakage-Various Stresses During Combing
11.4.4 INTRUMENTATION AND EXPERIMENTAL METHODS IN
STUDYING THE DAMAGE AND PROTECTION OF HAIR
1. Differential Scanning Calorimetry
Excessive thermal, chemical, weathering, and mechanical strains induce damage to the hair surface as well as the core of the fiber. Whereas surface analysis techniques, such as SEM, ToF-SIMS, and contact angle analysis, are all valuable in corroborating measurable stresses to the quality of the integument surface, thermoanalytical techniques, including Differential Scanning Calorimetry (DSC), may be used to probe the state of the subsurface fiber chemistry, such as the health of the cortical proteins.
The anatomy of a modern computer-controlled DSC instrument includes separate sample and reference holders, as well as vendor-specific cell closures, thermocouples, and gas purge inlets. The two principal types of DSCs are heat-flow and heat-flux instruments. Heat-flow instruments are based on the double-furnace design developed by Perkin-Elmer in the 1960s [15]. As a material passes through a thermal transition, the instrument uses local temperature readings and a feedback mechanism to ensure that the sample and reference pans are maintained at equivalent temperatures (i.e., TS=TR); hence, the amounts of power to the sample and reference furnaces are independent and are used to directly measure heat flow in or out of the sample. In heat-flux instruments, a single-furnace simultaneously heats both the reference and sample. Calibrations and temperature flow differences are then used to calculate heat flow during a thermal event (i.e., TS≠TR).
In a DSC experiment, the impact of thermal energy on phase transitions, such as melting (Tm) or glass transition (Tg) events, is logged as a function of applied temperature. Heating a sample causes changes in the ability of the material to hold onto thermal energy—where the increase in kinetic energy is distributed to optimize the vibrational, rotational, and translational states of the molecules that define motion within the material. The ability of a material to hold heat, which is called its heat capacity (Cp), is subsequently used to monitor excess, or differential, heat flow. Depending on the category of the thermal event, excess heat flows to the sample, or from the sample, relative to the empty sample pan. Put another way, to maintain the sample and reference cells at equivalent temperatures in a heat-flow instrument, excess energy is either added to (endothermic) or subtracted from (exothermic) the sample pan. For example, heating a thermoplastic polymer from subambient to the decomposition temperature will display the Tg and Tm events as endothermic; whereas crystallization and some curing processes appear as exothermic peaks (see Figure 3).
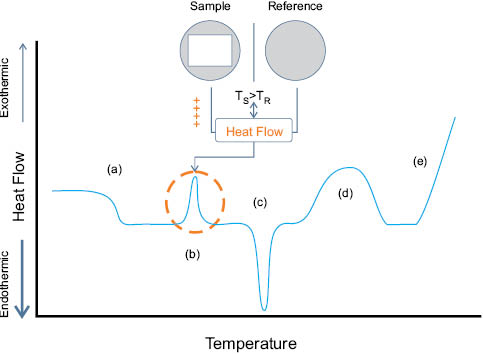
Figure 3: Peaks represent positive or negative heat flow (single-furnace). Characteristic DSC thermal transitions scanned from low to high temperature (exotherm points up): (a) glass transition temperature (Tg); (b) crystallization temperature (Tc); (c) melting temperature (Tm); (d) curing event; (e) thermal decomposition/oxidation (adapted from TA Instruments Thermal Analysis brochure, US).
In contrast to the aforementioned thermogram of a model synthetic thermoplastic, the human hair fiber is a very intricate composite and its intrinsic complexity typically adds intrigue to DSC data interpretation. Complexity aside, because applications of excessive heat, damaging chemicals, mechanical elongation, weathering strains, and combinations of each may alter the matrix cross-link density and/or irreversibly denature the secondary structure of the α-keratin to random coils and β-domains, DSC analyses of the endothermic denaturation temperature and enthalpy transitions are invaluable in quantifying the status of the stressed fiber cortex. That being said, consideration for the morphological complexity of a hair fiber is central in choosing whether to use “dry” or “wet” DSC methodology. In dry methodology, hair snippets are charged into a traditional, nonsealed aluminum DSC pan and water is evolved from the pan as samples are heated to decomposition. As a result, bookkeeping complexities arise as the denaturation (TD) and decomposition peaks inconveniently overlap into a poorly resolved doublet (between 230 and 250°C). However, the doublet may be happily resolved by testing in excess water and taking advantage of the water-plasticization of the matrix, which conveniently shifts the hair denaturation peak (120–150°) clear of interference from the 250°C pyrolysis peak [16]. This result begs the question: Why does water plasticization—which is a property typically affiliated with amorphous materials—influence the magnitude of TD for the crystalline α-helix?
The short answer is that water plasticity, in combination with prior chemical alterations, shifts the TD of the α-helix due to viscoelastic changes in the morphological components of the fiber composite. The cortex of human hair is principally compartmentalized into macrofibrils, microfibrils, and the cell membrane complex. Various researchers have further postulated kinetic and physical models to both simplify and relate the fiber chemistry and morphology to water plasticity and/or thermally induced phase changes [16–27]. For example, in Feughelman’s two-phase model (Figure 4) the intermediate filaments (IFs), or microfibrils, are composed of partially crystalline α-helical keratin bundles that are embedded in a highly cross-linked amorphous matrix [2, 17]. Typically, in most semi-crystalline polymeric materials, water interacts less with crystalline domains and more intrusively with amorphous, hydrophilic moieties; however, Wortmann suggests that, in human hair, water absorbs into the matrix and adsorbs to the periphery of the IFs equally well, meaning that water distributes within the cortex “quasi-homogeneously [18].” Therefore, as isolated IFs in hard keratins are soft and pliable when extended in water, it is clear that the surrounding matrix, which is also covalently bound to the IFs, plays a large part in the rigidity of hard keratins [16, 19]. Consequently, the two-phase model conveys that the magnitude of TD (i.e., thermal stability) for α-keratin is kinetically controlled by the cystine-based crosslink density and the viscosity of the nonhelical amorphous matrix, whereas the energy to denature (ΔHD) correlates with the structural rigidity of the α-helices in the IFs [20, 21]. In an augmented interpretation of the two-phase model, Istrate uses a variety of technical arguments to weigh the limitations of the Feughelman model. Instead, a third physical phase is introduced that links chemical changes (i.e., rate limiting S-S scission) in the nonhelical terminal domains of keratin filaments to the thermal stability of the IFs [22]. In a final example, Greenberg et al. studied hard keratins from various sources and concluded that an important function of the matrix is to keep the IFs in a semi-dehydrated state—suggesting that an intact matrix is key to maintaining the mechanical strength and stability of the IFs [19].
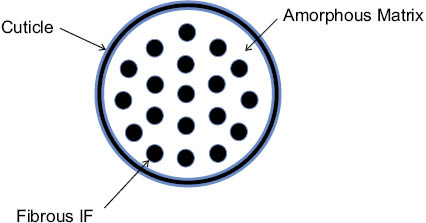
Figure 4: Diagram of a transverse section of hair fiber showing the traditional Feughelman (two-phase) morphological model where the composite fibrous intermediate filament(s) phase is immersed within a highly cross-linked amorphous phase.
As an illustration for the utility of DSC in evaluating cortical damage, Figure 5 shows the impact of hot flat ironing on virgin and polymer-treated fiber assemblies. The overlay was produced by following the methodology of Wortmann and Deutz [21]. Polymer-treated hair samples were prepared by applying model formulations to hair tresses. The tresses, including a freshly prepared virgin tress, were first blow-dried and next thermally treated with a timed regimen utilizing a high-temperature commercial flat-iron [4]. The virgin and thermally treated hair tresses were sectioned into small snippets and equilibrated at 60% RH overnight to normalize hydration history. Five to ten milligrams of the equilibrated snippets were subsequently charged into stainless-steel, pressure-resistant, large-volume DSC capsules, and 50 µL of water was added to each capsule. After sealing each pan, the hair snippets were hydrated overnight prior to charging into the DSC autosampler. In terms of the robustness/precision of the method, fastidious attention to the preparation protocol is critical to developing data worthy of inter-study (i.e., historical) comparisons. Specifically, art and tedium are intrinsic to the preparation of snippets, and variables such as water quality, heating rate, and application of all pretreatments must be precisely controlled.
Now that the hard part is done, it’s time to let the machine earn its keep. Depending on the thermal history, hydrated hair fibers characteristically denature between 110 and 150°C; hence, DSC investigations are accomplished by heating samples at 2–5°C/min over the 60–185°C temperature range. For example, thermograms a and e (Figure 5) depict the resultant outcomes of high-pressure DSC scans for wet, untreated virgin, and wet, thermally treated virgin hair snippets, respectively; and curves b-d and the trends in Table 2 show the effects of various commercially available polymeric pretreatments on the preservation of the secondary α-keratin structure. The diminishing magnitudes of the TD and ΔHD, which is the area of the endothermic peak after exposure of the hair tresses to the rigors hot flat-ironing, reflect the impact of thermally imposed strains on the integrity of the amorphous matrix and embedded α-helices. Chemically speaking, it has been suggested that the imparted stresses and subsequent shift in TD are related to a decrease in the matrix crosslink density, where the culprit is an increase in the number of thermally-induced disulfide bond scissions [22, 6]. Additionally, relative to flat-ironed virgin hair, the addition of selected polymeric treatments (e.g., b and c) to virgin fibers appears to mitigate the damaging effects of excessive thermal insult. Thus, for example, although the precise efficacy mechanism of “thermoprotective additives” is complex and currently debatable, the trends in Figure 5 and Table 2 suggest that treatment b is more successful than treatment d in hindering the irreversible progression of thermally induced α-keratin denaturation.
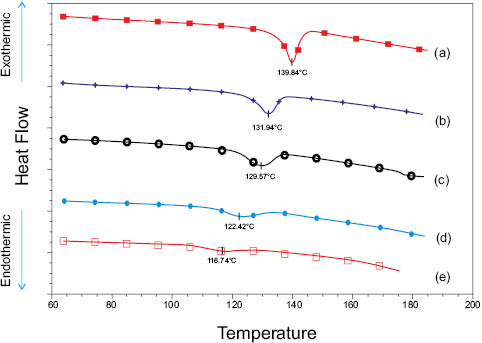
Figure 5: Effect of thermal styling treatment (232°C) on the α-helix melting temperature and associated enthalpy change (offset on y-axis for clarity). (a) Profile of untreated virgin hair; (b-c) flat-ironed hair/cationic polymer composites; (d) flat-ironed hair/non-ionic polymer composite; (e) flat-ironed virgin hair. Shifts in the peak minima from higher to lower temperature and decreased peak areas indicate presence of thermomechanically induced cortex damage (courtesy of D. Koelmel, Ashland Specialty Ingredients, US).
Table 2: Effects of thermal treatment on the denaturation temperature and denaturation enthalpy of European Dark Brown Hair
Sample Description | Shift in TD (°C) | ΔHD Loss (%) |
Virgin | — | — |
Flat-ironed + B-treated | 8 | 22 |
Flat-ironed + C-treated | 10 | 12 |
Flat-ironed + D-treated | 17 | 53 |
Flat-ironed Virgin | 23 | 81 |
Although thermal damage has been exemplified in portraying the merit of DSC methodology in measuring stresses in the fiber cortex, the influence of chemical [6, 17, 20, 22–26] and weathering strains [27], which also inflict damage to native cortical protein conformations, can also be discerned by DSC analyses. In extension, because the tensile mechanical properties of hair fibers are tied to the structural integrity of the cortex, thermal analysis enables a measurable connection between protein structure, bulk fiber performance, and the inception of novel keratin-preserving prototypes.
2. Surface Tension, Wetting, and Contact Angle Analysis
Interactions of a liquid and hair at the interface may be used to probe the physical and chemical states of the hair surface. The physicochemical state of the hair typically varies with hair length as weathering, cosmetic treatments, aging, and genetic strains induce measurable stresses on the fiber’s perimeter [28]. Depending on the extent, type, and location of damage, chemically unique segments of the F-layer, epicuticle, A-layer, exocuticle, endocuticle, cell membrane complex (CMC), and exposed cortex may all contribute to the measurable fiber-fluid interface. For instance, water is a very polar liquid and its wetting interaction with the hair surface depends on the summation of the accessible chemistry of the interface—explicitly, undamaged virgin hair fibers are lipophilic, whereas damaged fibers are on average more hydrophilic. Consequently, depending on the state of the hair, certain fluids tend to spread across the hair with film-like behavior, whereas others will bead on the surface, or form patchy domains on the hair’s heterogeneous landscape. Hence, the efficacy and performance of hair-damage repair treatments are affected by the current condition of the fiber, as well as the surface activity of the applied treatment formulation. Specifically, any treatment that lowers the tendency of the applied fluid to form cohesive and spherical droplets will increase the likelihood of that fluid wetting the hair surface. When done carefully, comparative measurements of the contact angle between the applied fluid and different substrates facilitate a description of comparative wetting behavior.
Insights into the likelihood of a fluid spreading across a surface may be gleaned by the parameters of the Gibbs equation (Eq. 1). Ignoring the intimidating squiggles of calculus, one only needs to focus on a couple of variables to see that surface tension (γ) is key to wetting a surface—and, via a mental extrapolation, that wetting is described by the magnitude of the contact angle of a fluid at the solid-liquid interface. The Gibbs equation relates the extent of adsorption of one phase (e.g., water) onto another (e.g., hair fiber) and suggests that a system that reduces the surface tension (γ), such as a surfactant, will have the propensity to be adsorbed onto a surface,
Γi= – 1/RT (∂γ/∂ln ai)T,P(1)
where Γi is the surface concentration of the spreading fluid, ai is the concentration of the adsorbing phase, T is the absolute temperature, and R is the gas constant.
Hence, prior to discussing the importance of contact angle in quantifying wetting processes on hair, it is useful to introduce surface tension, which, by dimensional analysis arguments, is equivalent to the surface free energy. As depicted in Figure 6, the atoms at the surface of a liquid are in a different environment than those in the bulk. Bulk molecules interact with neighboring molecules equally; however, the molecules at the surface of a liquid may only interact with neighboring surface molecules and with adjacent subsurface molecules. The net result of the asymmetry in attractive forces is that interfacial molecules are pulled inward until molecular collisions with bulk molecules arrest their contraction [29]. The surface is now analogous to a tight skin covering the bulk fluid, and the tight skin of the contracted interface requires energy to penetrate it or to extend its area. Thus, surface tension (or surface free energy, G), which has units of N/m (or J/m2), is defined as the force (or work) applied parallel to the surface of the fluid divided by the length (or area) over which it acts,
γ = F/l, or γ = (∂G/∂A)T,P,n(2)
where, in either form, Equation 2 infers that it requires energy (ΔG) to extend the surface (ΔA) and to bring molecules from the lower energy bulk to the stretched, higher-energy interface. Another way to view the surface ensemble is to envision that parameters affecting hydrogen-bond packing influence the cohesiveness and consequently tension of the interface. Conventionally speaking, the term “surface tension” is typically applied to forces at the liquid-vapor interface; because elastic forces confound and dominate the energy needed to expand the surface of a solid, measurements at the liquid-solid and vapor-solid interfaces are typically described by surface free energy.
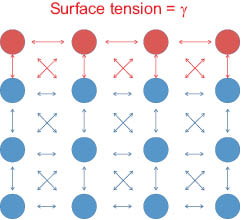
Figure 6: Model of an air-condensed phase interface.  =interfacial molecules.
=interfacial molecules.  =bulk molecules. The interfacial molecules are not solvated equally and are in a higher energy state than those in the bulk fluid.
=bulk molecules. The interfacial molecules are not solvated equally and are in a higher energy state than those in the bulk fluid.
Surface tension measurements are typically accomplished with a surface tensiometer and Wilhelmy Plate or du Noüy ring methods [30]. In surface tensiometry, the high-energy and pristine surface of the plate or ring is inserted into the solution to form a meniscus. As the probe is slowly removed, a microbalance follows the maximum force needed to overcome the wetting force, which is proportional to γ (or σ in Figure 7).
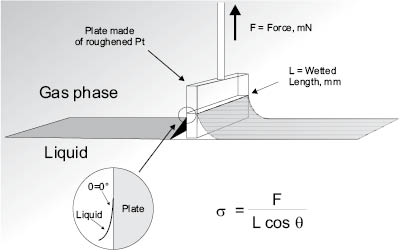
Figure 7: Wilhelmy plate method for determining surface tension. L=wetted perimeter; F=force exerted on microbalance; σ=γ=surface tension; θ=contact angle. θ is typically zero and, hence, cos 0 = 1 (courtesy of Krüss GmbH).
Wetting is an intuitive term and refers to the process of a liquid displacing a gas to make intimate contact with the surface of a solid. When interacting with a solid, poorly wetting liquids tend to bead, while exceptionally wetting liquids spread evenly across the exposed surface. The process of wetting a surface is related to the molecular interactions between the liquid and the solid. For example, if the liquid-liquid attractions within the droplet are stronger than the molecular attractions at the liquid-solid interface, the liquid will exhibit cohesive properties and will tend to bead at the surface of the solid. Conversely, if the molecules of the liquid and solid interact strongly, the liquid will counter adhesively by stretching its volume uniformly across the interface (Table 3).
Table 3: Description of cohesive and adhesive properties and relation to contact angle [courtesy of ramé-hart Instrument Co.]
Contact Angle | Wetting Description | Solid-Liquid Interaction | Liquid-Liquid Interaction |
0° | Complete | Strong | Weak |
60° | High | Strong | Weak |
90° | Moderate | Weak | Weak |
120° | Low | Weak | Strong |
180° | None | Weak | Strong |
The static contact angle of a fluid on a solid is typically measured with a modern Drop Shape Analyzer (DSA). In a DSA experiment, a sessile drop (i.e., liquid drop on solid) is carefully deposited on the substrate using a syringe. A mounted video camera is then used to capture an image of the drop on the surface, and accompanying image analysis software is used to measure the angle (i.e., contact angle) between the solid-liquid interface line and the tangent line at the liquid-gas interface. Figure 8 shows a water drop at equilibrium on a solid surface—a hair fiber. The equilibrium contact angle is the result of the sum of the interplay of three surface tensions, or surface energies: γsl is the surface tension of the solid-liquid interface, γsv is the surface tension of the solid-vapor interface, and γlv is the surface tension of the liquid-vapor interface. By definition, at equilibrium the vector sum of the three tensions, which sums along the parallel of the fiber-droplet interface, must be zero, and rearranging produces the Young equation (Eq. 3).
cos θ = (γsv – γsl) / γlv(3)
As indicated in Table 3, at θ > 90° the solid-liquid interface is at higher energy than the solid-air interface. In this instance, the vapor preferentially wets the surface and the liquid beads (i.e., minimal wetting). At θ = 0° (i.e., cos θ = 1) there is perfect wettability and, due to deviation from equilibrium, the Young equation no longer holds true [31, 32].
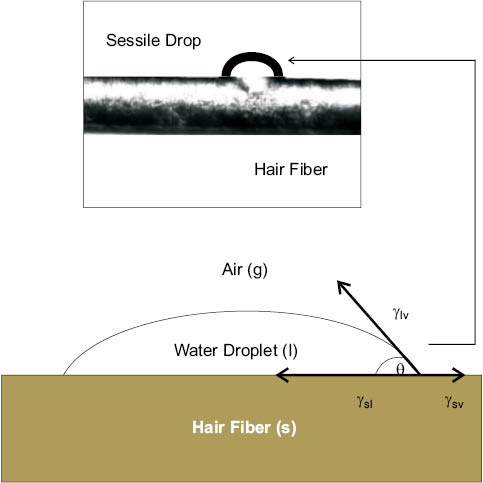
Figure 8: Top: 100 pL static water drop on surface of hair fiber (courtesy of Krüss GmbH). Bottom: Model of the interaction of liquid-vapor (γlv), solid-liquid (γsl), and solid-vapor (γsv) interfacial tensions.
The advantage of the sessile drop method is that multiple measurements on the sample surface may be used to gauge surface energy heterogeneity. That is, if measurements are done carefully, the variation between contact angle measurements will be indicative of the wetting variability as well as the gradation in surface topology as a function of x-y space. However, to make things interesting, by definition the static drop and associated Young equation apply to smooth and homogeneous surfaces; because a hair fiber is naturally porous, has variations in sebum and integral fatty acids, and has a jagged cuticular structure with natural and damage-dependent chemical and morphological inhomogeneity, good sense must be implemented when characterizing the meaning of the data and/or applying them to surface-free energy models. Further, DSA experiments are sensitive to droplet rearrangements (i.e., lateral motion), humidity, static electricity, volatility and/or sorption of the liquid—especially if applying low-volume droplet sizes to hair fibers. Hence, in the literature the use of the liquid drop method for determining contact angles on hair fibers is rather sparse.
Prior to recent advances (e.g., Figure 7) in video technology and drop volume [33] control, the application of DSA to the rough and chemically heterogeneous surface of hair rendered contact angle measurements difficult and unreliable [34]. Hence, historically speaking, the prevalent method in the literature for measuring the contact angle of a fluid at the interface with a single fiber is based on force tensiometry and the single-fiber Wilhelmy balance method. The Wilhelmy technique is considered a dynamic contact angle method because, unlike the sessile drop approach, the phase boundaries and shape of the meniscus are in perceivable motion as the fiber is advanced or receded from the fluid. In the application of the Wilhelmy method to hair, a small section of the hair fiber is affixed to a thin wire hook and suspended from the microbalance. The mass of the fiber is tared, and a moveable stage containing the fluid, such as high-purity water, is subsequently raised or (lowered) until a prescribed length of the fiber is submerged (e.g., 2–5 mm). As the fiber moves into the liquid, the wetting of the fiber produces a maximum force that is related to the advancing contact angle by Equation 4,
F = γP·cosθa,r + W – ρgyA,(4)
where F is the maximum measured force, P is the wetted perimeter of the fiber, θa is the advancing contact angle, ρ is the density of the fluid, g is the gravitational constant, y is the immersion depth, W is the weight of the fiber, and A is the cross-sectional area of the hair fiber [34]. The second and third terms of Eq. 4 are ignored because the fiber mass is initially tared, and because the buoyancy of a human hair is negligible. Subsequent retraction of the fiber from the fluid stretches the meniscus along the wetted fiber surface, and the maximum force produced is related to the receding contact angle (θr) by Eq. 4. Figure 9 depicts the Wilhelmy balance model and Figure 10 shows a force versus distance profile for a typical experiment. As with DSA, force tensiometry is sensitive to extraneous vibration, temperature fluctuations, and surface contamination. Also, for the Wilhelmy methodology, the wetting perimeter (Figure 11), the direction of scales (Figure 10 inset), and the rate of introduction or removal of the fiber from the interface affect equilibration processes and must be carefully controlled [35].
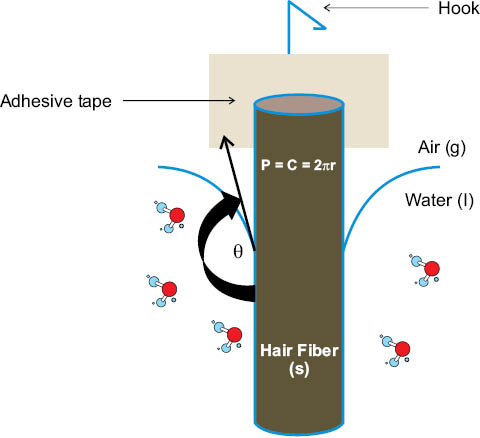
Figure 9: Diagram of dynamic contact analysis on hair using Wilhelmy methodology. Contact angle analysis is reduced from Eq. 7 to cos θ= F/γP, where P is the wetted perimeter of the solid, θ is the advancing or receding contact angle, and F is the wetting force corrected for buoyancy and fiber mass. P is approximately 2πr for a hair fiber.
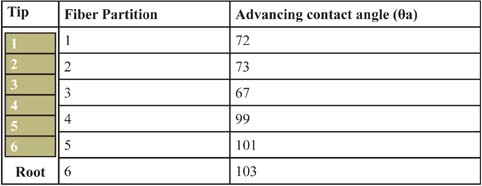
Kamath et al. [36] employed the Wilhelmy balance technique to study the effects of weathering, chemical, and mechanical insults on the water wettability of the fiber surface. The extent of daily mechanical strains and natural weathering processes (i.e., UV damage) was inferred by sectioning 10-inch-long fibers and next measuring the wetting forces as a function of root-to-tip distance. Table 4 suggests that daily UV and grooming processes introduce cuticular stresses that augment the hydrophilicity of a hair fiber as a function of time, or hair length. Hair that emerges from the scalp (zone 6) shows nonwettability properties, while zones 3–6, which are closer to the tip, show wettability traits similar to those seen in bleached fibers [34].
Table 4: Effect of root-to-tip distance on the magnitude of the advancing contact angle [38]
Using Wilhelmy techniques, Molina et al. [37] studied the impact of chemical strains on the physicochemical properties of the integument. They evaluated the application of alkaline solutions with and without 0.6% H2O2 and compared to untreated hair. Because hydrogen peroxide is known to oxidize cystine to cysteic acid residues, the assumption is that this influences the hydrophilicity as well as the number of ionizable moieties on the cuticular surface. Attempts were made to augment wetting trends by characterizing the physical (dispersive) and chemical (acid-base) contributions to the work of adhesion across the interface,
WSL = WSLLW + WSLAB,(5)
where WSL is the equilibrium work of adhesion, WSLLW is the Lifshitz-van der Waals (i.e., dispersive or hydrophobic) component, and WSLAB is the contribution of acid-base interactions between the liquid and solid. WSLAB may subsequently be solved for by applying Equation 6 to the empirical data [37],
WSLAB = λL(1 + cos θ) – 2(λLLW · λSLW)1/2,(6)
where λL is the surface tension of the dry solid, λLLW is the dispersive component of the surface tension for the liquid, and λSLW is the dispersive component of the surface tension for the dry solid. Not surprisingly, the results confirmed that untreated hair is less wettable than alkaline-treated and/or peroxide treated fibers. Further, by controlling the aqueous pH during tensiometry measurements, it was shown that alkaline-treated fibers have an increase of ~2 times increase in WSLAB, and oxidized fibers have an increase of 3–4 times increase in WSLAB relative to untreated fibers—confirming that alkaline and/or oxidative treatment increases the number of hydrophilic and ionizable functionalities on the hair surface.
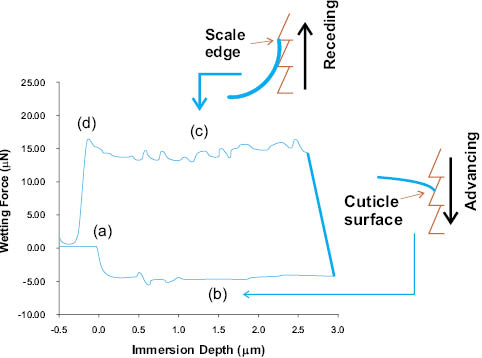
Figure 10: Wetting force as a function of immersion depth for a virgin hair fiber. The fibers are typically mounted in the against-scale direction. (a) Fiber penetrating the liquid interface; (b) fiber advancing into liquid surface; (c) fiber receding from interface; (d) meniscus breaks from fiber. The insets depict one reason for contact angle hysteresis (θa-θr). During advancing of fiber into liquid, the meniscus interacts with cuticle surface; in the receding step, the meniscus strongly adheres to scale edges [34, 36, 37, 39].
Using Zisman’s approach [38] to find the critical surface tension (λC), where plotting cos(θ) versus λlv with test liquids and extrapolating to θ=0 to find λC, Kamath [37] detailed the λC wetting argument into dispersive and polar terms,
λC = λdS + λpS,(7)
where λC is the critical surface tension, and λdS=24 mN/m and λpS=4 mN/m are the polar and dispersive components for untreated hair, respectively. The low-magnitude dispersive component reflects the dominating average hydrophobic nature of virgin hair, and also intimates that very high surface tension fluids will bead on the pristine hair surface. However, intuitively, the ensuing chemical effects of oxidation significantly increase λC and λpS– and, therefore, increase the likelihood of additional homogenous chemisorption interactions between higher surface tension conditioners, such as water-soluble cationic polymers, and the modified higher-energy surface.
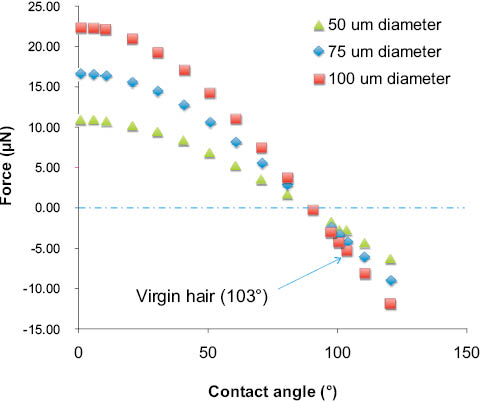
Figure 11: Consequence of the magnitude of the wetting perimeter on the profile of the force curve (see Eq. 4). Nonwetting solids are less dependent on fiber diameter. Virgin hair has a negative wetting force, and θA is approximately 103° [34, 36, 37].
Kamath et al. [35], and also Lodge and Bushan [34], studied the wetting properties of virgin, chemically treated, and subsequently conditioned, hair tresses. Lodge observed a statistically significant (p=0.05) reduction in the dynamic contact angle (Wilhelmy balance) with permanent waving (70±7°) and with the application of conditioner (88±9°) to virgin hair (103±4°); however, application of commercial conditioner to permed hair (79±1°) caused an increase in the contact angle, relative to the permed hair. To explain the trends, both Kamath and Lodge speculated that the state of the fiber may dictate how the conditioning surfactant associates with the hair. For example, on damaged hair, the cationic groups will electrostatically bind more strongly to the copious cysteic acid moieties and the lower-energy alkyl chains of the surfactant will be directed towards the surface (i.e., higher contact angle, decreased wetting). Yet, on application of cationic conditioner to virgin hair, with a presumably intact F-layer, the hydrophobic alkyl chains of the surfactant may physisorb with the bound lipids and the higher-energy cationic moieties will be exposed to the surface (i.e., lower contact angle, increased wetting).
Lodge [34] also rationalized that contact angle hysteresis (H = θa – θr) could be used to study the location of the deposition of conditioners on a hair fiber. Relative to the permed-fiber curve, very little contact angle hysteresis was seen for the bleached-and-treated fiber. This indicated that the conditioner deposited significantly on the cuticle edges, producing a larger θr than expected because the intrinsic hydrophilicity of the scales was “hidden.” This result was corroborated by Dupres et al. [40, 41], who used noncontact AFM to examine the microscopic heterogeneity of wetting behavior for a range of solvents on hair fibers—including silicone oil (21 mN/m), decane (23 mN/m), and squalane (31 mN/m). Results indicated that only silicone oil wets the hair surface completely; however, the cuticle edges, which are proteinaceous and more hydrophilic than the cuticular surface, were wet homogenously by the oils (Figure 12). Using critical surface tension arguments, this clearly suggests that the cuticle edges have a higher λC than the cuticle surface, and that the hydrophobic oils have λ less than the λC of the cuticle edge.
Trends in surface tension, wetting, and contact angle trends are valuable tools for following the deleterious effects of chemical, mechanical, thermal, and weathering strains on the integrity of the cuticle. Due to chemical and surface heterogeneity, hair fibers are a challenging substrate for both static and dynamic contact angle measurements. Advances in DSA technology have rendered small-volume, sessile-drop DSA measurements on single fibers feasible, although the surface heterogeneity of hair renders challenges to evaluating instrument precision. Due to an abundance of examples in the literature, the Wilhelmy balance method is still the established method for measuring the wettability of single fibers. By employing surface energy models to contact angle results, it is possible to gain insight into the chemical modifications of the surface and to accordingly develop treatments to ameliorate the compromised wetting properties of damaged hair.
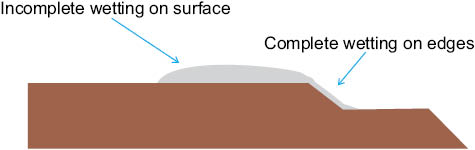
Figure 12: Preferential wetting of virgin hair by squalane. Squalane spreads uniformly across the relatively polar cuticle edge, whereas sparse wetting is visible on the hydrophobic cuticle surface.
3. Dynamic Vapor Sorption (DVS)
Prior to the advent of commercialized Dynamic Vapor Sorption (DVS) technology, the interaction of relative humidity (RH) with a sample was principally studied by exposing pre-dried samples to isothermal air over a series of saturated salt solutions (42). Samples were then periodically removed from the desiccators and weighed to study sorption kinetics and to obtain the equilibrium sorption isotherm. Understandably, the methodology was both tedious and time consuming due to the lack of automation. Furthermore, it was more difficult to accurately monitor the rate of sorption and to strictly control the environment of the samples within the cumbersome desiccators—including temperature, dry gas type, sorbent vapor type, vacuum, and the logistics of transferring highly hygroscopic materials between the desiccator and balance.
In general, modern DVS analysis is a fully automated, gravimetric technique used to monitor the interaction of a gaseous probe molecule (e.g., water, cyclohexane) with a substrate of interest (e.g., polymer film, hair). The relative vapor pressure (i.e., RH for water vapor) is accurately controlled by streaming a mixture of dry (e.g., nitrogen, air) and vapor-saturated gases in correct proportions using mass flow controllers. The mass changes of the sample are monitored with an ultra-sensitive microbalance, and changes in the chemistry of the sample can be simultaneously followed with NIR spectroscopy, Raman spectroscopy, and/or optical microscopy. Depending on the instrument model, one or several very small samples (< 30 mg) can be dried at 0% RH, pre-heated to high temperatures (e.g., 100–300°C), pre-humidified, cooled or heated, exposed to stepped or oscillating humidity, or influenced by reduced pressures—all automated and all in situ. Because all aforementioned processes can be programmed into the DVS control software using sequences, and without altering the position or controlled environment of the sample, both equilibrium and kinetics trials may be used to fully differentiate comparative sorption processes. During water vapor DVS analysis, which is the method typically used in the literature to study interactions with hair fibers, the relative humidity in the sample compartment is varied stepwise with time and changes in mass are continuously monitored. A subsequent plot of the equilibrium sorbed vapor mass (i.e., mass regain) against the relative humidity at a controlled temperature is termed a sorption isotherm. The resulting hysteresis plots, which are generated by plotting the mass difference between the sorption and desorption isotherms at each isohume, are insightful in contrasting characteristic substrate traits such as equilibrium moisture content, bound versus unbound water, surface hydrophobicity, and porosity. Although fully equilibrated experiments are inherently time consuming for porous or swellable biomaterials, proper equilibration between the adsorbent (substrate) and adsorbate (vapor) facilitates the determination of accurate equilibrium moisture contents and diffusion coefficients. In addition, application of comparative isotherm data to theoretical sorption models may be used, albeit controversially (43), to visualize the allocation of adsorbed and absorbed vapor at the surface and within, respectively, a porous substrate—such as a hair fiber.
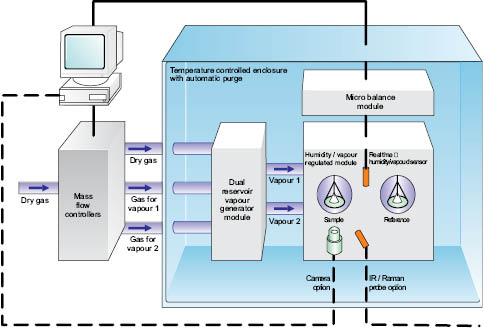
Figure 13: Modern DVS Instrumentation (courtesy of Surface Measurement Systems, UK).
Hair fibers are hygroscopic, yet an undamaged hair fiber with endogenous sebum and intact integral fatty acids has a low surface tension and effectively repels water (44). Although contradictory, the net result is that hair has a penchant for slowly absorbing and slowly desorbing water vapor, as indicated by its characteristic sigmoidal DVS isotherm and noted hysteresis between the sorption and desorption steps. The hysteresis lag and the exothermic heats of sorption suggest that once water negotiates a path through the cuticle and into the cortex (i.e., absorbed water) it is tightly held by the hydrophilic peptide residues within the fiber (45). As absorbed water induces radial swelling of the fiber and affects the free volume and mobility of α-keratin, any treatment that affects hair’s water transport processes will induce transient changes in properties such as dye mobility and mechanical strength (46). Hence, DVS analysis is a tool to forecast the impact of weathering and the efficacy of protective or repair remedies on the quality and health of a keratinous fiber.
Bleaching and perming are processes that impart chemical strains to the hair. Bleaching is a harsh oxidizing process, whereas perming involves the reduction of disulfide bonds followed by an oxidative process to reform the bonds in a newly styled position. Barba et al. (47) contrasted the water transport processes of untreated, bleached, and permed natural red hair using DVS. Subsequent fitting of the sorption data to the Guggenheim, Andersen, and De Boer (GAB) sorption model was used to calculate the GAB monolayer capacity (Wm) and GAB energy constant (Cg) (48, 49). Loosely speaking, Wm relates the number of vapor-binding sites to the mass of hair; Cg is related to the enthalpy of sorption, and is a measure of how strongly water vapor adheres to the binding sites in the hair fiber (50). The GAB sorption model is an enhanced BET sorption model and has been shown to give a physics-based connection between the water absorbed and the number of hydrophilic sites on the substrate (51).
Table 5: DVS Results from Sorption Studies on Untreated, Bleached, and Permed Natural Red Hair by Barba et al. (46)
Hair | Max. Regain, 95% RH (%) | Wm (%) | Cg | tT (min) | DA (min-1) |
Untreated | 25.87 | 7.487 | 6.706 | 3204.22 | 0.0163 |
Bleached |








