3D Mechanical Modeling of Facial Soft Tissue for Surgery Simulation

State of the art medical image acquisition, image analysis procedures and numerical calculation techniques are used to realize a computer model of the face capable of realistically represent the force-deformation characteristics of soft tissue. The model includes a representation of the superficial layers of the face (skin, superficial musculoaponeurotic system, fat), and most facial muscles. The whole procedure is illustrated for determining geometrical information, assigning mechanical properties to each soft tissue represented in the model, and validating model predictions based on a comparison with experimental observations. The capabilities, limitations and possible future use of this approach are discussed.

Computer-based design and simulation methods enable engineers to optimize functionality, reliability, manufacturing process, and costs of new devices and machines. To this end, computer models are developed that represent the three-dimensional (3D) geometry of the system, the interaction of its parts, the changes in shape caused by the application of loads, as expected in the different conditions of service. Recent improvements in the procedures for 3D geometric data acquisition and representation, advances in the understanding and the mathematical description of the force-displacement relationship in the case of large deformations and nonlinear time-dependent behavior of materials, and the continuous enhancement in the performance of modern computer systems have allowed application of this approach to complex design problems, such as, for example, the optimization of the crash resistance behavior of a car. Application of computer-based design and simulation procedures to medical problems is one of the main objectives of current research in biomechanics. Examples of recent developments are simulations of trauma, calculations for predicting the outcome of surgery, real-time simulations for intraoperative navigation, and surgical training using virtual reality. This article presents the 3D numerical model of the face developed in our laboratory at ETH Zurich for simulation of soft facial tissue response to physiologic loads, and for investigation of plastic and reconstructive surgery procedures and devices.

Modeling the changes in shape of the face caused by the application of external force vectors or internal (muscle) contractions is a challenging mechanical problem. It requires an accurate representation of the anatomic elements, their interactions, the kinematic boundary conditions (ligament fixations), and the nonlinear and time-dependent force-deformation characteristics of all involved tissues and organs. Although numerical models were intended initially to realize realistic animations of facial expressions (eg, Terzopoulos and colleagues ), more detailed representation of face anatomy and the force-deformation characteristics were developed for simulations related to the physiology and pathology of face deformation, such as for modeling human mastication, facial outlook or expressions of emotion in craniofacial and maxillofacial surgery planning, and for the prediction of the outcome of reconstructive surgery after burns injuries.

The so-called finite element (FE) method is a calculation tool that provides accurate simulations of the mechanical behavior of deformable bodies. The large computational time associated with FE calculations has motivated the development of alternative numerical approaches allowing for fast (in certain cases, even real-time) surgery simulation, such as mass-spring or mass-tensor models. FE models are often used as the benchmark for evaluation of the predictive capabilities of these simplified numerical algorithms (see, eg, Mollemans and colleagues ).

FE models of the face proposed in the literature were mostly based on the external contour of the face and the shape of the bones. In the study by Keeve and colleagues, uniform mechanical properties for soft facial tissue were applied. Chabanas distinguished 2 layers and modeled 4 muscles using elements running through the layers. Zhachow and colleagues and Gladilin and colleagues proposed a more accurate model from the anatomic point of view: magnetic resonance images were segmented to extract the shape of 18 face muscles, which were embedded into homogeneous soft tissue. The muscles were activated through the definition of a contractile force acting in the direction of predefined muscle fibers. Active muscle behavior was considered also in the work by Nazari and colleagues for simulation of orofacial movements.

In most of these models, linear elastic material behavior is assumed for soft facial tissue. Nonlinear mechanical model equations are required in the case of large deformations of facial tissue (see, eg, Har-Shai and colleagues ). Mazza and colleagues used hyperelastic-viscoplastic constitutive equations with internal variables (including a so-called aging function) to simulate gravimetric descent such as that resulting from a progressive loss of stiffness of the aging facial tissue. The corresponding FE model consists of 4 layers of uniform thickness obtained from laser scan data of the external face surface.

Although still far from the realization of computer models capable of quantitative and reliable patient-specific prediction of surgical outcome, today’s numerical simulations, with an increasing level of realism, are intended to provide objective criteria for comparison of alternative surgical procedures, improve visualization and prediction of soft tissue deformation for surgery planning and intraoperative navigation, and to complement trials on cadavers and clinical studies for the development of new tools for plastic and reconstructive surgery. This article reports on the development of a 3D FE model of a face designed to give a faithful representation of (1) the anatomy, (2) the mechanical interactions between different tissues, and (3) the nonlinear force-deformation characteristics of all tissues. The model presented in this paper is one of the most accurate numerical models of the face available so far. The geometry of each anatomic part is based on reconstructions from magnetic resonance images; shape, constraints, and interactions of tissues and organs have been verified to be consistent with state-of-the-art knowledge on face anatomy; nonlinear constitutive equations are used for modeling the mechanical behavior of each tissue.

The procedure for model generation is presented, including the reconstruction based on segmented contours of the anatomic parts, the realization of the corresponding FE mesh for numerical simulations, the anatomic aspects considered for defining kinematic boundary conditions, and interactions between the anatomic parts. The mechanical model equations used for describing the mechanical behavior of facial tissues are introduced later in this article. Materials parameters were initially selected based on data from the literature. Specific information on the mechanical behavior of the face being investigated was obtained from a series of experiments. The response of facial tissues to gravity loads and to the application of a measured pressure inside the oral cavity has been quantified using magnetic resonance images and holographic techniques and compared with the results of the corresponding FE calculations. Information on the local mechanical response of the superficial soft tissue (skin, superficial musculoaponeurotic system [SMAS], and superficial fat) in different regions of the face, was obtained using suction experiments (Cutometer and aspiration device). Results of predictions of gravimetric soft tissue descent will be presented as an example of application of the face model. Aging predictions were evaluated comparing the contour of the simulated aged face with the results of contour extraction from frontal photos of volunteers at different ages. This article also includes a discussion of the capabilities and limitations of the present model and an outlook to possible applications and further development of this approach.

Model development

Representation of Bones, Muscles, Tissue Layers, Ligaments

High-resolution magnetic resonance imaging (MRI) data were acquired for determination of the shape of bones, soft layers, and muscles. This procedure is commonly used to generate 3D anatomic models. Using a Philips Achieva 1.5T scanner, 150 slices at a distance of 2 mm with an in-plane resolution of 0.5 mm were obtained for the head and neck of a 27-year old man lying in the supine position. The high quality of images obtained resulted from an iterative optimization considering acquisition time and ability of the tested person to maintain a relaxed position, without muscular contractions. Fig. 1 shows an example of a transverse MRI image.

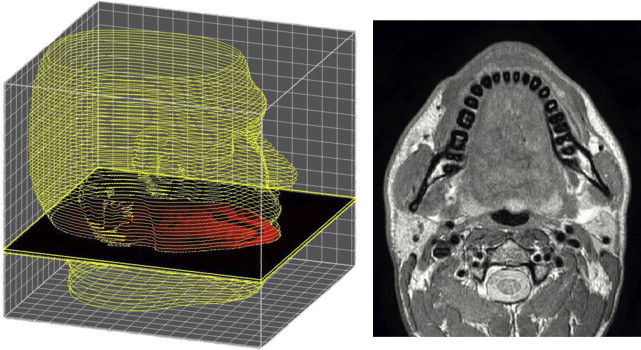
The most challenging step for extraction of geometric data to be used in the FE model is the segmentation and reconstruction of all anatomic elements. Skull and mandibula could be obtained using a semiautomated procedure based on a simple threshold segmentation algorithm, with manual adjustments applied to separate mandibula and skull in the articulation temporomandibular (ATM) region, and upper and lower teeth. The good contrast and resolution of the MRI images allowed in this case a quick and reliable reconstruction of bones, for which computed tomography scans are usually preferred. The definition of the external contour of the face was almost fully automated, requiring only minor adjustments.

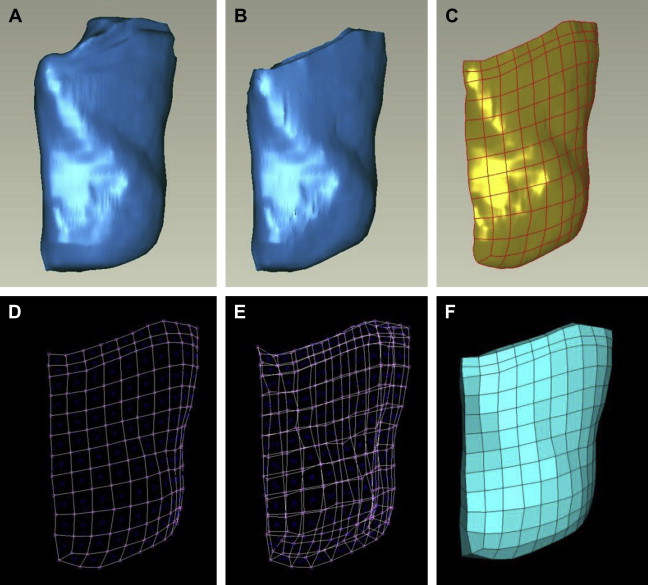
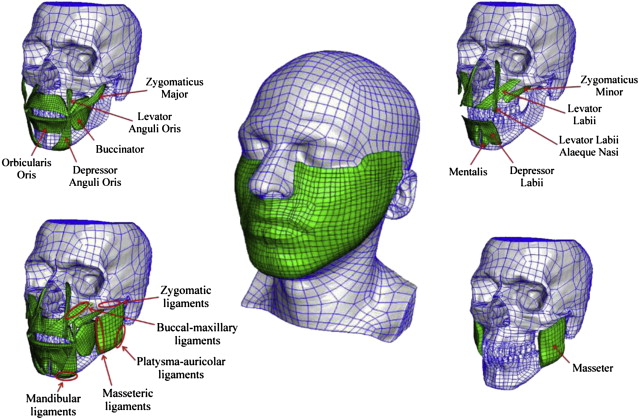
Reconstruction of the muscles was obtained through a time-consuming procedure, illustrated in Fig. 2 for the case of the masseter muscle. The commercial software AMIRA (Konrad-Zuse-Zentrum Berlin, Mercury Computer Systems) was used for segmentation and reconstruction of each anatomic part. The software creates a polygonal surface model of each segmented feature. The triangulated surface is imported into the commercial software package Geomagic Studio (Geomagic, Inc., Triangle Park, NC) for a manual correction of incomplete parts. The FE model is then created based on this geometry (discussed later). All muscles required manual segmentation and reconstruction; in regions where they intersect or run close to each other, a manual separation of the contours had to be made. Identification of the muscle boundaries in some cases needed the evaluation of information from literature and consultation with anatomy experts. Not all muscles and local tissue parts were modeled, to limit both the effort related to anatomy extraction and the computational power, which increases with model complexity. Barbarino and colleagues describe the selection of the muscles to be included in the model along with the considerations related to their relevance to the mechanical behavior of the face. As indicated in Fig. 3 , the following muscles were included in the model: buccinator, zygomaticus major and minor, levator anguli oris, levator labii, levator labii alaeque nasi, depressor labii, depressor anguli oris, mentalis, and masseter. Orbicularis oris, risorius, temporalis, and pterygoidei medialis and lateralis are among the muscles neglected in the present model.

Skin (epidermis and dermis) is modeled with a soft layer of constant thickness (2 mm, an average of the values observed in the MRI images) covering the whole face. Mucosa is a continuous layer, similar in structure to the skin. It was thus modeled with the same thickness as the skin. The SMAS is an important structure for plastic surgery, but there is not a consistent anatomic definition of this layer. The MRI images did not allow the SMAS to be distinguished from deeper connective tissue. The model assumption adopted was therefore to introduce the SMAS along with the superficial fat as a homogeneous layer parallel to the skin with a general thickness of 3 mm. The thickness of this layer has been suitably reduced in different regions to not overlay muscles or bones. This procedure led to a nonuniform layer interfacing the skin to muscle, bone, or deeper connective tissue. Further details concerning the representation of SMAS and platysma muscle are reported by Barbarino and colleagues.

Soft tissue deeper to the SMAS was represented as filler of the empty spaces in between mucosa, muscles, SMAS, and skin, with properties determined by the large number of fat cells included in this tissue. All interfaces are modeled as tied contacts (no sliding, no separation).

Retaining ligaments are not explicitly represented in the FE model, but their effect is considered in terms of boundary conditions: following the nomenclature of La Trenta, zygomatic, mandibular, and platysma-auricular ligaments were modeled by constraining the displacement of the corresponding regions of the FE model (see Fig. 3 ). The masseteric-cutaneous ligaments were modeled by locally increased resistance to deformation for the connective tissue between the anterior border of the masseter muscle and the skin.

Generation of the FE Mesh

The FE calculation of face deformations is based on a local definition of the relationship between forces and displacements. The so-called mesh is composed of elements geometrically defined by the nodes located at the outer boundaries of each element. Depending on the mechanical properties of the material, the forces applied at the nodes are transmitted through adjacent elements, and result in node displacements and element deformations. The computational time is proportional to the number of degrees of freedom, and thus to the number of elements and nodes. The FE mesh of the face was defined with the objective of creating a model with sufficient spatial discretization, providing good performance in terms of computational time and accuracy. A semiautomatic procedure has been applied that generates a mesh composed of hexahedron elements starting from an object in the form of a triangulated surface.

As illustrated in Fig. 2 , each object is divided in parts with a simple geometry (close to a parallelepiped) and a basis surface is defined for each part. The surface is subdivided in patches using a grid of splines and a quadrilateral surface mesh is generated. This two-dimensional (2D) mesh is extruded by an average thickness of the part, thus creating a 3D hexahedron mesh. Then, an algorithm is used to project the nodes of this mesh to the original triangulated surface of the object. Manual adjustments are often required to correct distorted elements or to increase the correspondence with the object geometry at some locations. The mesh of each object is then imported into the commercial software ABAQUS (Simulia, Providence, RI), used as solver and postprocessor for the FE calculations (see Fig. 3 for the whole numerical model).

Model Equations for the Mechanical Behavior of Soft Facial Tissue

The local relationship between forces (stresses) and deformation is defined for each material through the so-called constitutive equations. Har-Shai and colleagues evaluated the nonlinear viscoelastic mechanical properties of skin and SMAS with experiments on excised tissue samples. Corresponding constitutive equations were developed by Rubin and Bodner. The original model considers history-dependent variables and corresponding evolution equations to reproduce the observed mechanical response caused by the microscopic morphology of the tissues. A direct link between tissue microstructure and macroscopic mechanical behavior cannot be achieved at present. Instead, the equations and the material parameters are determined by comparing predictions of the model with macroscopic experimental data. The constitutive model was implemented as a user-defined algorithm into the commercial FE software ABAQUS (Papes O, PhD thesis, in preparation), and used for aging simulations by Mazza and colleagues.

The model formulation by Rubin and Bodner was applied to all tissues of the present face model, with a specific model parameter set for each tissue. Steady response of facial tissue was considered in the experiments and corresponding simulations. For this reason, the parts of the model that describes short-term, transient, and dissipative behaviors were neglected for the calculations performed so far. Further details on the model equations as applied to the present face model are reported by Barbarino and colleagues.

Five material parameters have to be assigned to each facial tissue. The values selected for this face model were those reported in literature. Note that no material parameter fitting was performed to match simulations and experimental observations that are reported later in this article. Because of the high water content, all tissues were assumed to have a density of 1000 g/cm ³, except for the skin, with a value of 1100 g/cm ³, in accordance with the measurements reported by Duck. Rubin and Bodner determined model parameters of skin and SMAS by fitting experimental data. The same assumptions we reported in 2005 were used here to define mechanical properties of mucosa and deep fat; the material constants of the mucosa were taken to be the same as those of the skin, because they have a similar structure. For the deep fat, the stiffness was taken to be 1 order of magnitude less than the SMAS. Mechanical properties of muscles were selected to provide a factor of 10 higher value of the stiffness compared with SMAS. For simplicity, muscles were selected as passive isotropic tissue.

Local measurements of the mechanical response of the superficial layers of the specific face modeled in this work were performed, providing specific values for the corresponding model parameters (discussed later).

In all simulations, skull, mandibula, and the parotid gland have been modeled as rigid bodies, because these parts are stiffer than all other facial tissues considered in the model.

Experimental observation and simulation of face deformation

The FE model as described earlier can be used for simulation of face deformation for specified force applications, related to physiologic conditions of loading or to medical intervention. The uncertainties of the simulation results are related to model assumptions such as (1) constitutive model parameters, (2) spatial discretization (mesh density), (3) boundary conditions (ligaments, fixations), and (4) organ interactions. The purpose of the experiments reported here was to compare simulations with physical reality and thus evaluate the predictive capabilities of the model, and to provide further information on the mechanical behavior of the face for improvement of the FE model. MRI and holographic measurements were used to determine the change in shape of the face consequent to the application of simple (and known) distributed mechanical loads or given displacements. The so-called pull-up experiment was applied to analyze the response to the application of a force vector. Suction measurements were performed to locally determine the mechanical behavior of skin and SMAS in different regions of the face.

MRI Measurements

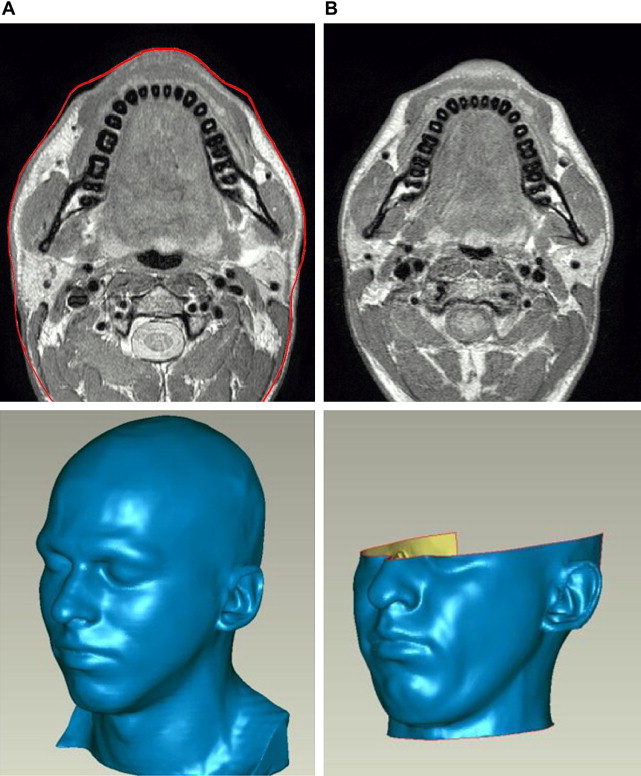
Deformation of the face caused by gravity was analyzed using MRI scans taken with the tested person lying (1) in the supine position facing the ceiling, (2) horizontally facing the floor. Fig. 4 compares corresponding transversal sections for scans (1) and (2). The effect of gravity was quantified by computing the shortest distance between the whole skin surfaces for cases (1) and (2). The same procedure was applied to determine skin surface displacements for corresponding FE simulations of a distributed gravity field with a magnitude of 2 × g, corresponding to the difference between configurations (1) and (2). Measurements and FE calculations are compared in Fig. 5 showing a good qualitative correspondence in the distribution of the deformation, with the calculated values lower than the measurements, indicating a too-stiff behavior of the model. Note that no adjustment of material parameters was applied for these results.

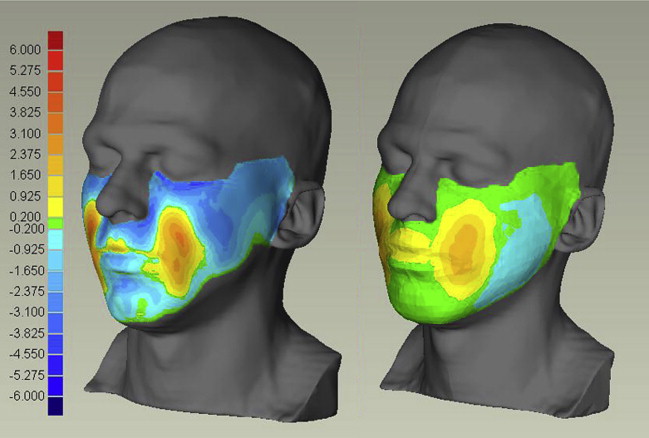
MRI measurements with 2 wooden balls with a diameter of 2.5 cm inserted between the cheeks and the tooth were conducted to analyze the model response to a known imposed internal deformation. Fig. 6 shows a representative transversal section for this case and compares the MRI scan with the corresponding numerical results. The simulation considered the wooden balls as rigid bodies placed inside the oral cavity and displaced to the final position in contact with the mucosa. The calculated external surface displacement and the internal distribution of deformations agree to a great extent with the experiment. The redistribution of connective tissue (deep fat and SMAS) is well represented and the corresponding displacements of the buccinator and masseter muscles confirm the selection of the corresponding boundary conditions. Differences are evident toward the lips region, probably related to the muscles being modeled as passive, whereas a contraction of the orbicularis oris muscle is necessary to keep the lips closed.

Holographic Measurements

In holographic measurements, phase and intensity information are recorded from the interference pattern of light reflected from the observed surface and reference light from the same source. The analysis of these data allows determination of the 3D surface shape of the face with short acquisition time and high resolution.

Two measurements have been performed: (1) with the tested person standing vertically in front of the holographic camera system with no face muscle contractions; (2) in the same position, but with a tube inserted between the lips and the subject blowing into it with a relative pressure of approximately 10 mbar (measured with a pressure sensor connected with the tube). The result of this experiment was the displacement field as the distance map between the face surfaces (1) and (2), Fig. 7 B. Using the same color code, Fig. 7 C reports the result of the corresponding FE simulation with overpressure applied inside the oral cavity. The comparison shows good qualitative correspondence, with the FE model providing lower displacement.