Since the number of negatively charged electrons is equal to the number of protons in the nucleus, the atom itself is electrically neutral.
The electron shells are characterised by discrete amounts of the binding energy. Transitions of electrons between these energy levels or orbits are accompanied with emission or absorption of discrete portions of energy. Since the Coulomb attraction between the negative electrons and the positive nucleus decreases with increasing distance, the inner electrons are more tightly bound, i.e. they have a higher binding energy. The number of protons Z equals the atomic number and thus determines the chemical element of the atom as well as the structure of the electron shells. The number of protons in the nucleus is the same for all atoms of a given element, but the number of neutrons may vary. These atoms, with a different number of neutrons, but the same number of protons, are called isotopes.
Since the number of the elementary particles in the nucleus is responsible for the atomic weight, we can define the mass number A as
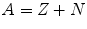
While the chemical behaviour of an atom is only determined by its atomic number, the properties of the atomic nucleus depend on the number of neutrons too. In nuclear physics a certain nucleus is denoted as follows:
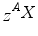 with A, Z, and X being the mass number, the atomic number, and the chemical symbol of the element, respectively. Examples are 919F, 2960Co, 92238U denoting isotopes of the elements fluorine, cobalt, and uranium with 19, 60, and 238 nucleons, respectively. Because the atomic number Z and the chemical element provide redundant information, the subscript often is omitted. Atomic nuclei can be stable as well can disintegrate, thereby forming new nuclei with different properties. This behaviour of an atomic nucleus to decay within a given time is what we call radioactivity. We know different types of the radioactive decay, each characterised by the emission of specific particles: α-, β−-, and β+-particles.
with A, Z, and X being the mass number, the atomic number, and the chemical symbol of the element, respectively. Examples are 919F, 2960Co, 92238U denoting isotopes of the elements fluorine, cobalt, and uranium with 19, 60, and 238 nucleons, respectively. Because the atomic number Z and the chemical element provide redundant information, the subscript often is omitted. Atomic nuclei can be stable as well can disintegrate, thereby forming new nuclei with different properties. This behaviour of an atomic nucleus to decay within a given time is what we call radioactivity. We know different types of the radioactive decay, each characterised by the emission of specific particles: α-, β−-, and β+-particles.
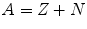
(2.1)
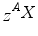
The α-decay is usually observed for heavy nuclei with a big neutron excess. α-particles are atomic nuclei of helium, consisting of two protons and two neutrons. The equation for the α-decay can be written as
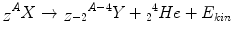
Typical examples are the decay of 235U to 231Th as well as 226Ra to 222Rn.
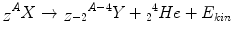
(2.2)
The β−– and the β+-decay occur for medium-weight isotopes with neutron or proton excess respectively. To describe the β−-decay, the following equations apply:
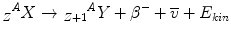
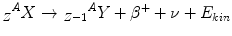
β− and β+ indicate an electron and a positron, respectively; the positron is the anti-particle of the electron with the same mass but an electrical charge of opposite sign. ν and ν− denote the neutrino and the antineutrino, respectively, which are particles without mass and charge, and a very low probability to interact with matter. Radionuclides emitting β-radiation are, for example, 90Sr which decays to 90Y by emission of β−-radiation and the positron emitting 19F. The daughter nucleus originating as a result of an α or β-decay might exist in an excited energy state. To return to the ground state, the nucleus has to de-excite which usually happens by emitting discrete amounts of energy as γ-radiation. From the physical point of view, γ-radiation is electromagnetic radiation with a very high frequency, but can also be regarded as particles – so-called γ-quanta – having no rest mass and no electric charge. γ-emitting radionuclides are widely used as radiation sources in radiotherapy.
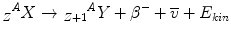
(2.3)
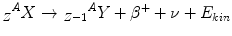
(2.4)
Radioactive nuclei decay randomly. If we have a sample of nuclei, and we consider a time interval short enough to assure that the population of atoms did not change significantly by decay, then the proportion of atoms decaying in our short time interval will be proportional to the length of the interval. The number of nuclei N which have not yet decayed after an arbitrary time interval t follows an exponential law:
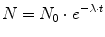
where N 0 is the number of radioactive nuclei at time 0 and λ is known as the radioactive decay constant characteristic for the particular decay. The rate of disintegration of any radioactive substance is commonly designated by its half-life T ½, which is the time required for one-half of a given quantity of the substance to decay. Depending on the element, a half-life can be as short as a fraction of a second or as long as several billion years. Substituting the decay constant by the half-life according to
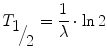
we get
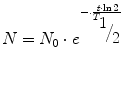
The activity A is the physical quantity used to measure the rate of disintegration. The unit of activity is 1/s (s−1) which means one decay per second and is called Becquerel (Bq). For instance, in a sample of an activity of 1 MBq, 1,000,000 nuclei decay in every second. Since the number of decaying nuclei, i.e. the activity, is proportional to the number of radioactive nuclei, we can express the exponential law of decay also in terms of activity by simply substituting N by A.
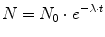
(2.5)
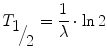
(2.6)
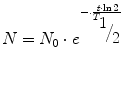
(2.7)
2.2 The Nature of Ionising Radiation
Atoms in general – as stated above – are electrically neutral. When an atom or molecule is ionised, it acquires or loses one or more electrons. Ionisation by removing electrons can among other things be caused by bombarding atoms with charged particles like α- and β-particles as well as by uncharged particles like neutrons or γ-quanta. In general, radiation means energy that is radiated or transmitted in the form of rays or waves or particles. Ionising radiation is high-energy radiation capable of producing ionisation in the substances through which it passes.
If the energy lost by the incident radiation is not sufficient to detach an electron from the atom, but is used to raise an electron from its energy level to a higher one, this process is called excitation.
Table 2.1 summarises different types of ionising radiation. Since all charged particles ionise atoms by themselves, they are called direct ionising radiation. Uncharged particles like neutrons and photons, i.e. electromagnetic radiation at high energies, ionise matter by charged particles produced by only a few interactions with atomic electrons or nuclei. These secondary particles actually detach the prevailing majority of electrons from the atoms. That is the reason why we call uncharged particles also indirect ionising radiation. From the point of view of radiotherapy, photons are the most important indirect ionising radiation. As mentioned above, photons are electromagnetic radiation. We know electromagnetic waves from our daily life, e.g. as radio waves, microwaves, visible, and ultraviolet light.
Table 2.1
Possible classification of ionising radiation
Ionising radiation | ||
|---|---|---|
Indirect (uncharged) | Direct (charged) | |
γ-rays, X-rays (photons) | Neutrons | Electrons, positrons (β-particles) α-particles, protons, ions |
Rest mass = 0 | Rest mass >0 | |
Electromagnetic waves or quantum radiation | Particle radiation | |
Waves are characterised by their frequency f, their wavelength λ, and their velocity of propagation c (which is the speed of light for electromagnetic waves) according to the following relation:
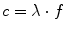
However, they can also be regarded as particles with a defined energy E and a rest mass being zero:
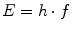
The factor h is known as Planck’s constant. The production of which will be explained later, and the γ-radiation emitted by excited nuclei are electromagnetic waves at very high frequencies.
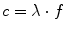
(2.8)
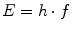
(2.9)
The unit to measure the energy of elementary particles, electrons, and photons is the electron volt (eV). It is the energy gained by a particle which carries one elementary charge as it traverses a difference in electrostatic potential of one volt in vacuum. The electron volt is a very small unit:
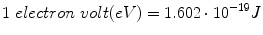 Since mass is a form of energy, the masses of elementary particles are sometimes expressed by electron-volts; e.g. the mass of the electron, the lightest particle with measurable rest mass, is 511 keV/c 2, where c is the speed of light.
Since mass is a form of energy, the masses of elementary particles are sometimes expressed by electron-volts; e.g. the mass of the electron, the lightest particle with measurable rest mass, is 511 keV/c 2, where c is the speed of light.
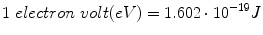
The eV is a useful energy unit when discussing atomic processes as its magnitude is adapted to the low energy levels involved.
In the following, the essential interactions of ionising radiation with matter will be discussed.
2.2.1 Interaction of Charged Particles with Matter
If any charged particles such as electrons penetrate matter, they produce ionisation by collision with the atoms. Charged particles interact with the orbital electrons as well as with the electromagnetic field of the atomic nucleus. The radius of the nucleus is about 10−14 m, and the radius of the electron orbits is about 10−10 m. For this relation of size, we can imagine that the probability that any charged particle travelling through matter interacts with an orbital electron is bigger than hitting the nucleus. The energy of the incident particle is transmitted to many atoms in a large number of collisions along the particle track through the medium. Thus, the primary particle will lose its energy by a large number of small increments.
As the incoming particle interacts with the orbital electrons, it causes ionisation or excitation. These interactions are mediated by the Coulomb force between the electric field of the moving particle and the electric field of the orbital electrons. When the path of the incoming particle is deflected by the electrostatic attraction of the nucleus, it results in an energy loss of the incident particle with the lost energy being emitted as electromagnetic radiation. Because of the underlying mechanism, this radiation is called bremsstrahlung, which is a German word and means “braking radiation”. Both electronic collisions and the production of bremsstrahlung cause a decrease of the kinetic energy of the charged particles, as the depth of the penetrated tissue grows, until they stop. As a consequence, charged particles have a limited range in matter. The physical quantity that describes the process of slowing down of charged particles is the stopping power S. The stopping power is defined as the ratio of lost energy per path length. To eliminate the influence of the mass density especially for compound materials, usually the mass stopping power S ρ is used:
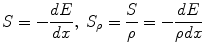
Because of their different masses, electrons, protons, and heavier particles have different ranges in matter. It can be seen that for the penetration of several centimetres into water which is equivalent to soft tissue protons must have kinetic energies of several hundred MeV, whereas a few MeV are sufficient for electrons. Electrons of such energy can be generated with reasonable effort by linear accelerators, which will be discussed later, whereas the production of protons with therapeutically relevant ranges requires huge particle accelerators. Therefore, electrons are the most commonly charged particle radiation used for radiotherapy.
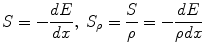
(2.10)
The collision of high-energy electrons and heavy charged particles like protons, deuterons, or α-particles with atomic nuclei can lead to nuclear reactions, too. Since this kind of interaction is of no importance for the objective of this book, it will not be considered further on.
2.2.2 Interaction of Uncharged Particles with Matter
2.2.2.1 Basic Effects
Uncharged particles are also denoted as indirectly ionising radiation (cf. Table 2.1) because they generally ionise matter in two steps. Since photon radiation is the only indirectly ionising radiation used for the radiotherapy of benign diseases, just the interactions of photons with matter will be discussed in the following. The primary interaction of photons with matter is characterised by the release of electrons with kinetic energies big enough to ionise atoms directly. These secondary electrons behave like primary electrons, i.e. they are slowed down by electronic collisions and bremsstrahlung production and have a limited range depending on their kinetic energy as shown above. The kinetic energy itself depends on the energy of the primary photon as well as on the type of the interaction. For photon radiation with energies in the range from about 10 keV up to several MeV, which are relevant for radiotherapy, the following effects are of importance:
Rayleigh or coherent scattering
Photoelectric effect
Compton effect or incoherent scattering
Pair production
Photo disintegration, where photons release neutrons or protons from atomic nuclei, is observed for photons with energies greater than about 10 MeV, only, and is of less importance in radiotherapy [1].
Coherent or Rayleigh scattering means that only the direction of the primary photon is influenced as a result of the interaction with bound electrons. There is no energy transferred to the interacting atom; hence the energy of the incident photon remains unchanged. In compound materials, consisting of elements with low atomic numbers like biological tissue, coherent scattering occurs mainly for photons with energies below about 20 keV.
The photoelectric effect or photoabsorption is observed when the incoming photon detaches an inner shell electron. The incident photon disappears, thereby dividing its energy into two parts: one part is used to release the bound electron and the other part is given as kinetic energy to it. The created inner shell vacancy is filled by an electron from an outer shell whereby the excessive binding energy is emitted as electromagnetic radiation. The energy of these monoenergetic photons depends on the difference in the binding energies of the two involved electron shells. Because the binding energies of the electron shells are characteristic for the particular atom, i.e. for the particular element, the emitted radiation is referred to as characteristic photon radiation. If the energy of this photon is transferred to an outer shell electron, then a so-called Auger electron will be ejected. The probability to undergo photoabsorption strongly increases with the atomic number and decreases with photon energy. The photoelectric effect is the dominating interaction in biological materials for photon radiation with energies up to about 50 keV.
In the Compton effect, individual photons collide with single electrons that are free or loosely bound in the atoms. Incident photons transfer a part of their energy and momentum to the electrons, which in turn recoil. In the instant of the collision, new photons of less energy are produced that scatter at angles, the size of which depends on the amount of energy lost to the recoiling electrons. These deflections of the primary photons, accompanied by a change of their energy, are known as Compton scattering. The probability of the occurrence of the Compton effect has only a very weak dependence on the atomic number and decreases slightly with the photon energy. The Compton effect dominates in light elements like biological tissue in the energy range from about 50 keV up to several MeV.
If the energy of the incident photon exceeds 1,022 keV, then an electron and a positron together can be created in the strong Coulomb field of the atomic nucleus. The rest mass of an electron and a positron, respectively, is equivalent to an energy of 511 keV each. Hence, this pair production can only occur if the photon has an energy which at least amounts to twice that mass equivalent. The difference between the photon energy and that threshold energy of 1,022 keV is converted into kinetic energy of the electron and the positron. After the positron has been nearly stopped, it annihilates with an arbitrary electron under emission of two radiation quanta with an energy of 511 keV each. Pair production, like the photoelectric effect, exhibits a strong increase in the interaction probability with atomic number, but tends to increase with photon energy, too. Pair production must be taken into account for photon energies above several MeV especially for heavy elements.
2.2.2.2 Exponential Attenuation Law
As a consequence of the photon interactions described above, not only secondary electrons that ionise additional atoms are being produced, but the properties of the incident photon field are being altered, too. Either the primary photon disappears completely (photoabsorption, pair production) or it is scattered with (incoherent) or without (coherent) energy loss. In other words, the primary photon beam is attenuated. This attenuation depends on photon energy and on the following material parameters: thickness, density, and atomic number. For narrow, monoenergetic photon beams the attenuation can be described by an exponential law given in the following equation:
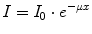
where
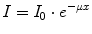
(2.11)
I Intensity of the photon beam after passing through the material with thickness x
I 0 Intensity of the photon beam before passing through the material
x Material thickness
μ Linear attenuation coefficient.
Dividing the linear attenuation coefficient by the mass density, we obtain the mass attenuation coefficient μ/ρ which does not depend on density. However, in the above formula the linear thickness has to be replaced by the mass thickness ρx:
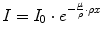
The total mass attenuation coefficient μ/ρ is composed of the individual coefficients for the single processes described above:
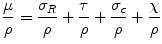
σ Ρ/ρ is the attenuation coefficient for the coherent scattering, τ/ρ for the photoelectric effect, σ Χ /ρ for the Compton effect, and χ/ρ for pair production. As mentioned above, all these effects depend on the atomic number of the attenuation material and on the energy of the photon beam. This means that one or two effects dominate the attenuation processes for a given combination of matter and energies. Since photon radiation between a few tens of keV and several MeV is used for radiotherapy, the Compton effect is obviously predominant except for low photon energies. The total attenuation coefficient varies only slightly with photon energy within the interval between 1 and 10 MeV and is nearly independent on the material. Photon attenuation is dependent of energy – the curves become more flat with increasing energy, indicating a decreased attenuation.
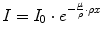
(2.12)
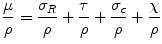
(2.13)
2.2.3 Inverse-Square Law
Any point source which spreads its influence equally in all directions without a limit to its range will obey the inverse-square law. This follows from the law of conservation of energy, because the flux of radiation through a spherical surface imagined around a radiation source has to be constant (no energy is created or lost outside the source, i.e. there are no interactions with matter). Being strictly geometric in its origin, the inverse-square law applies to ionising radiation as well. As the surface of a sphere of radius r is given by 4πr 2, the radiation intensity has to decrease with 1/r 2 so that energy is conserved. Correspondingly, the amount of radiation received by an object at a distance r decreases with 1/r 2, i.e. the inverse square of the distance from the source. Thus, the inverse-square law can be written as
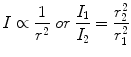
with I 1, I 2 being the intensity of radiation at distances r 1 and r 2, respectively.
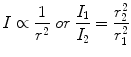
(2.14)
2.2.4 Dosimetric Quantities
In the preceding paragraphs, we concentrated on the basic interactions of radiation. The energy lost by radiation of any kind travelling through matter is transferred directly or indirectly via charged secondary particles to a large number of atoms. This physical process of energy deposition is the origin of all chemical, biochemical, and biological alterations in biological tissue. To quantify the biological consequences of ionising radiation, a measure is needed which provides a sufficiently reliable relation between the amount of applied radiation and the biological effects and which can be determined reproducibly. The quantity that fulfils these requirements is the energy dose. The energy dose D is defined as the ratio of the energy dE deposited by ionising radiation in matter per unit mass dm:
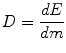
The SI unit for the energy dose is J/kg which we also call a Gray (Gy):
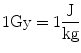




(2.15)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








